题目内容
已知椭圆的长轴长为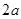 ,焦点是
,焦点是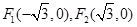 ,点
,点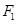 到直线
到直线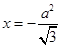 的距离为
的距离为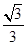 ,过点
,过点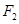 且倾斜角为锐角的直线
且倾斜角为锐角的直线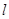 与椭圆交于A、B两点,使得|
与椭圆交于A、B两点,使得|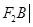 =3|
=3|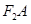
 .
.
(1)求椭圆的标准方程;
(2)求直线l的方程.
(1) 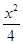 +y2=1;(2)
+y2=1;(2)  x-y-
x-y-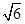 =0.
=0.
解析试题分析:(1)∵F1到直线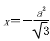 的距离为
的距离为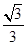 ,∴
,∴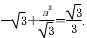 .
.
∴a2=4而c=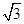 ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为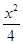 +y2=1 4分
+y2=1 4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知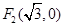
 =3
=3 ,
,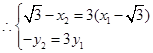
∴
 6分
6分
∵A、B在椭圆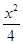 +y2=1上,
+y2=1上,
∴l的斜率为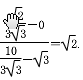
∴l的方程为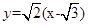 ,即
,即 x-y-
x-y-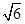 =0. 12分
=0. 12分
说明:各题如有其它解法可参照给分.
考点:本题主要考查椭圆的标准方程、几何性质,定比分点坐标公式,直线方程。
点评:中档题,涉及求椭圆的标准方程问题,往往联想椭圆的定义,a,b,c,e的关系。求直线方程,这里运用了点斜式,为求直线的斜率,应用定比分点坐标公式及“点差法”。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的右焦点为
的右焦点为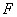 ,右准线为
,右准线为 ,离心率为
,离心率为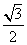 ,点
,点 在椭圆上,以
在椭圆上,以 为半径的圆与
为半径的圆与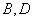 .
.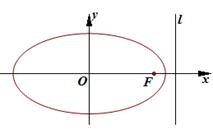
 是边长为
是边长为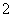 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;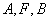 三点在同一条直线
三点在同一条直线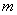 上,且原点到直线
上,且原点到直线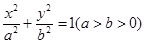 的左右焦点分别为
的左右焦点分别为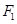 、
、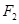 ,由4个点
,由4个点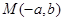 、
、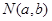 、
、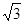 ,面积为
,面积为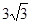 的等腰梯形.
的等腰梯形.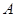 、
、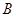 两点,求
两点,求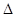
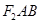 面积的最大值.
面积的最大值.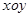 和极坐标系
和极坐标系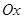 的原点与极点重合,
的原点与极点重合, 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线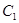 的极坐标方程为
的极坐标方程为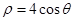 ,曲线
,曲线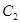 的参数方程为
的参数方程为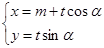
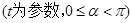 ,射线
,射线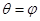 ,
,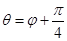 ,
,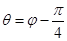 与曲线
与曲线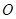 以外的三点A,B,C.
以外的三点A,B,C.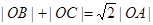 ;
;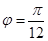 时,B,C两点在曲线
时,B,C两点在曲线 与
与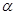 的值。
的值。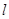 :
: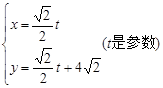 上的点向圆C:
上的点向圆C: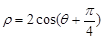 引切线,
引切线,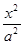 +
+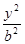 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F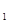 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y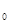 ,y
,y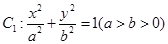 的离心率为
的离心率为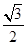 ,
,
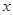 轴被抛物线
轴被抛物线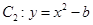 截得的线段长等于
截得的线段长等于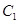 的长半轴长.
的长半轴长.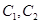 的方程;
的方程;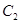 与
与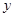 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线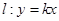
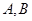 两点,直线
两点,直线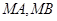 分别与
分别与 .
. 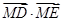 为定值;
为定值;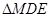 的面积为
的面积为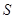 ,试把
,试把 的函数,并求
的函数,并求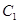 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为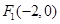 ,
,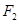
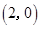 ,点
,点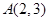 在椭圆
在椭圆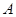 的直线
的直线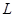 与抛物线
与抛物线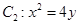 交于
交于 两点,抛物线
两点,抛物线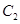 在点
在点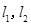 ,且
,且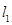 与
与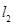 交于点
交于点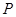 .
.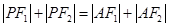 的点
的点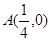 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若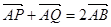 ,
,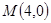 .
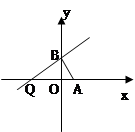
.
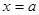 ,以PM为直径的圆与直线
,以PM为直径的圆与直线