题目内容
已知函数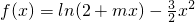 .
.
(1)若f(x)在 处取得极值,求m的值;
处取得极值,求m的值;
(2)若以函数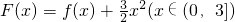 图象上任意一点P(x0,y0)为切点的切线的斜率
图象上任意一点P(x0,y0)为切点的切线的斜率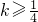 恒成立,求正实数m的最小值;
恒成立,求正实数m的最小值;
解:(1)∵函数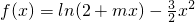 .
.
∴f′(x)=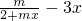
∵f(x)在 处取得极值,
处取得极值,
∴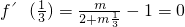
∴m=3
(2)根据题意:F(x)=ln(2+mx)
∴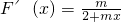
∴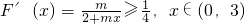 恒成立,
恒成立,
转化为:m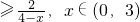 恒成立
恒成立
∴m≥
∴正实数m的最小值是 .
.
分析:(1)由函数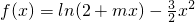 ,可求得f′(x)=
,可求得f′(x)=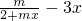 ,再由f(x)在
,再由f(x)在 处取得极值,建立
处取得极值,建立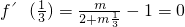 ,求解m.
,求解m.
(2)根据题意:F(x)=ln(2+mx),则有∴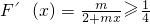 ,x∈(0,3)恒成立,转化为:m
,x∈(0,3)恒成立,转化为:m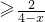 ,x∈(0,3)恒成立,只要求得
,x∈(0,3)恒成立,只要求得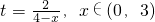 最大值即可.
最大值即可.
点评:本题主要考查函数与方程的综合运用,还考查了不等式恒成立问题和函数最值的求法.
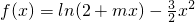 .
.∴f′(x)=
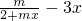
∵f(x)在
 处取得极值,
处取得极值,∴
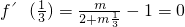
∴m=3
(2)根据题意:F(x)=ln(2+mx)
∴
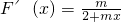
∴
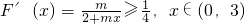 恒成立,
恒成立,转化为:m
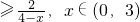 恒成立
恒成立∴m≥

∴正实数m的最小值是
 .
.分析:(1)由函数
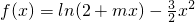 ,可求得f′(x)=
,可求得f′(x)=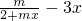 ,再由f(x)在
,再由f(x)在 处取得极值,建立
处取得极值,建立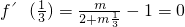 ,求解m.
,求解m.(2)根据题意:F(x)=ln(2+mx),则有∴
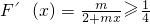 ,x∈(0,3)恒成立,转化为:m
,x∈(0,3)恒成立,转化为:m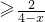 ,x∈(0,3)恒成立,只要求得
,x∈(0,3)恒成立,只要求得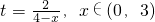 最大值即可.
最大值即可.点评:本题主要考查函数与方程的综合运用,还考查了不等式恒成立问题和函数最值的求法.

练习册系列答案
相关题目
 .
. .
. .
. .
. .
. .
. .
.