题目内容
现有200根相同的钢管,把它们堆放成正三角形垛,要使剩余的钢管尽可能的少,那么剩余钢管的根数为( )
分析:由题意可知正三角形垛各层的钢管数组成一个首项为1,公差是1的数列,由此得Sn=
<200.解出使不等式成立的n的最大值,再求剩余的钢管数即可选出正确选项
| n(n+1) |
| 2 |
解答:解:∵把200根相同的圆钢管堆放成一个正三角形垛,
∴正三角形垛各层的钢管数组成一个首项为1,公差是1的数列,
∴正三角形垛所需钢总数为Sn=1+2+3+4+…+n=
,
令 Sn=
<200,
解得n=19是使得不等式成立的最大整数,此时Sn取最大值190,由此可以推出剩余的钢管有10根.
故选B.
∴正三角形垛各层的钢管数组成一个首项为1,公差是1的数列,
∴正三角形垛所需钢总数为Sn=1+2+3+4+…+n=
| n(n+1) |
| 2 |
令 Sn=
| n(n+1) |
| 2 |
解得n=19是使得不等式成立的最大整数,此时Sn取最大值190,由此可以推出剩余的钢管有10根.
故选B.
点评:本题考察数列的应用,考查了等差数列的确定及其求和公式,解题的关键是理解题意得出各层钢管数是一个等差数列,由题设中所给的问题转化出合适的概率模型是解题的难点.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 B.
B.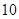 C.
C.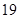 D.
D.