题目内容
已知三次函数f(x)=x(x-a)(x-b) 0<a<b
(1)当f(x)取得极值时x=s和x=t(s<t),求证:o<s<a<t<b;
(2)求f(x)的单调区间.
答案:
解析:
解析:
|
解(1)∵f(x)=x3-(a+b)x2+abx 由题意S,t为 又∵ ∴ 又∵s<t ∴0<s<a<t<b 解(2)由上(1)可知x<s时 x>t时 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
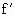 (x)=3x2-2(a+b)x+ab
(x)=3x2-2(a+b)x+ab .从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是
.从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是 ,出现绿灯的概率是
,出现绿灯的概率是 ;若前次出现绿灯,则下一次出现红灯的概率是
;若前次出现绿灯,则下一次出现红灯的概率是 ,出现绿灯的概率是
,出现绿灯的概率是 .问:
.问: