题目内容
若a、b、c是正实数,则关于x的方程:8x2-8| a |
| b |
| c |
分析:根据题意,首先假设三个方程都没有两个不等实根,则
,将三式相加得a+b+c≤0,与已知条件a、b、c是正实数相矛盾,即可得原命题成立.
|
解答:证明:假设三个方程都没有两个不等实根,则
,
三式相加得:32(a+b+c)≤0,
即a+b+c≤0与已知a、b、c是正实数,矛盾.
故至少有一个方程有两个不相等的实数根.
|
三式相加得:32(a+b+c)≤0,
即a+b+c≤0与已知a、b、c是正实数,矛盾.
故至少有一个方程有两个不相等的实数根.
点评:本题考查反证法的运用,注意反证法中常见的推导矛盾的方法,如相加、相乘等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
A.选修4-1:几何证明选讲
|
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
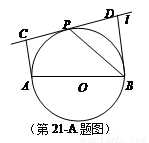
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
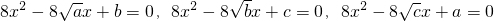 至少有一个方程有两个不相等的实数根
至少有一个方程有两个不相等的实数根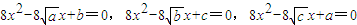 至少有一个方程有两个不相等的实数根
至少有一个方程有两个不相等的实数根