题目内容
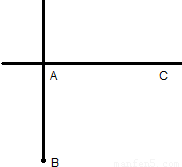如图，两条铁路线垂直相交于站A，已知AB=100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以v公里/小时的速度从B站沿BA方向行驶至A站，在乙火车从B站到A站的过程中．（1）用V表示甲、乙两车的最近距离（两车的车长忽略不计）；
（2）若从开始行驶到甲、乙两车相距最近时，所用时间为t小时，问V为何值时，t最大．
【答案】分析：（1）设乙车行驶t小时到D，甲车行驶t小时到E，分类讨论，利用二次函数确定最值；
（2）利用基本不等式，即可求得结论．
解答：解：（1）设乙车行驶t小时到D，甲车行驶t小时到E
若0≤vt≤100，则DE2=AE2+AD2=（100-vt）2+（50t）2=（2500+v2）t2-200vt+10000
∴
时，DE2取到最小值，DE也取到最小值，最小值为
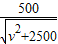
若vt＞100，乙车停止，甲车继续前行，DE越来越大，无最大值
综上，甲，乙两车的最近距离为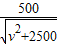
公里；
（2）
=
≤
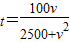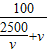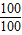=1，当且仅当
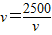，即v=50公里/小时，t最大
点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．
（2）利用基本不等式，即可求得结论．
解答：解：（1）设乙车行驶t小时到D，甲车行驶t小时到E
若0≤vt≤100，则DE2=AE2+AD2=（100-vt）2+（50t）2=（2500+v2）t2-200vt+10000
∴
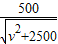
时，DE2取到最小值，DE也取到最小值，最小值为若vt＞100，乙车停止，甲车继续前行，DE越来越大，无最大值
综上，甲，乙两车的最近距离为
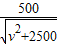公里；（2）
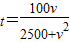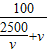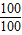=≤=1，当且仅当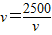，即v=50公里/小时，t最大点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．
练习册系列答案
相关题目
（2006•宝山区二模）如图，两条铁路线垂直相交于站A，已知AB=100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以v公里/小时的速度从B站沿BA方向行驶至A站，在乙火车从B站到A站的过程中．