题目内容
某工厂有旧墙一面长14米,现准备利用这面旧墙建造平面图形为矩形,面积为126平方米的厂房,工程条件是:①建1米新墙的费用为a元;②修1米旧墙的费用是问如何利用旧墙,即x为多少米时,建墙费用最省?(1)(2)两种方案哪个更好?
分析:以建墙费用为目标函数,通过讨论函数的最小值来解决本题.
解:设利用旧墙的一面矩形的边长为x,则矩形的另一面边长为![]() 米.
米.
(1)利用旧墙的一段x米(x<14![]() 为矩形一面边长,则修旧墙费用为x·
为矩形一面边长,则修旧墙费用为x·![]() 元,将剩余的旧墙拆得的材料建新墙的费用为(14-x)·
元,将剩余的旧墙拆得的材料建新墙的费用为(14-x)·![]() 元,其余建新墙的费用为(2x+
元,其余建新墙的费用为(2x+![]() -14)·a元.故总费用为y=
-14)·a元.故总费用为y=![]() ·a+
·a+![]() ·a+(2x+
·a+(2x+![]() -14)·a=a(
-14)·a=a(![]() +
+![]() -7)=7a(
-7)=7a(![]() +
+![]() -1)(0<x<14),
-1)(0<x<14),
∴y≥7a[2![]() -1]=35a,当且仅当
-1]=35a,当且仅当![]() =
=![]() 即x=12米时,ymin=35a.
即x=12米时,ymin=35a.
(2)若利用旧墙的一面矩形边长为x米(x≥14),则修旧墙的费用为![]() ·14=
·14=![]() a元,建新墙的费用为(2x+
a元,建新墙的费用为(2x+![]() -14)a元,故总费用为y=
-14)a元,故总费用为y=![]() a+(2x+
a+(2x+![]() -14)a=
-14)a=![]() a+2a(x+
a+2a(x+![]() -7)(x≥14).
-7)(x≥14).
∴y′=2a(1-![]() )=
)=![]() ,当x≥14时y′>0.
,当x≥14时y′>0.
∴函数y=![]() a+2a(x+
a+2a(x+![]() -7)在[14,+∞]上为增函数.故当x=14时,
-7)在[14,+∞]上为增函数.故当x=14时,
ymin=![]() a+2a(14+
a+2a(14+![]() -7)=35.5a.
-7)=35.5a.
综上讨论知:采用第(1)方案,利用旧墙12米为矩形的一面边长时,建墙总费用最省,为35a元.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
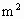 的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为
的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为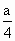 元;③拆去1m旧墙,用所得材料建1m新墙的费用为
元;③拆去1m旧墙,用所得材料建1m新墙的费用为 元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好? 的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为
的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为 元;③拆去1m旧墙,用所得材料建1m新墙的费用为
元;③拆去1m旧墙,用所得材料建1m新墙的费用为 元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好? 元;②修1米旧墙的费用为
元;②修1米旧墙的费用为 元;③拆去1米旧墙用所得材料建1米新墙的费用为
元;③拆去1米旧墙用所得材料建1米新墙的费用为 元.经过讨论有两种方案:⑴利用旧墙的一段x(x<14)米为矩形厂房的一面边长;⑵矩形厂房的一面长为x(x≥14).问如何利用旧墙,即x为多少米时,建墙费用最省?⑴⑵两种方案哪种方案最好?
元.经过讨论有两种方案:⑴利用旧墙的一段x(x<14)米为矩形厂房的一面边长;⑵矩形厂房的一面长为x(x≥14).问如何利用旧墙,即x为多少米时,建墙费用最省?⑴⑵两种方案哪种方案最好?