题目内容
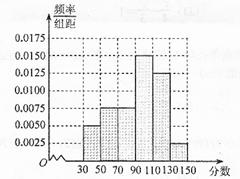
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组 ,第2组
,第2组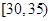 ,第3组
,第3组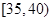 ,第4组
,第4组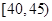 ,第5组
,第5组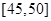 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
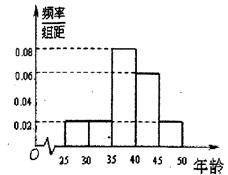
(1)上表是年龄的频率分布表,求正整数 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人年龄在第3组的概率.
(1)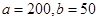 ;(2)第1,2,3组分别抽取1人,1人,4人;(3)
;(2)第1,2,3组分别抽取1人,1人,4人;(3)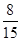 .
.
解析试题分析:本题考查频率分布直方图的读法、分层抽样以及随机事件的概率等基础知识,考查学生的分析能力和计算能力.第一问,根据频率分布直方图求频率;第二问,考查分层抽样,利用样本容量比总容量的比例计算;3.利用第2问的结论,列出所有可能情况,在其中挑出符合题意的情况,求比值.
试题解析:(1)由频率分布直方图可知,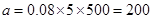 , 2分
, 2分 . 4分
. 4分
(2) 因为第1,2,3组共有50+50+200=300人,利用分层抽样在300名学生中抽取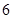 名学生,每组抽取的人数分别为:
名学生,每组抽取的人数分别为:
第1组的人数为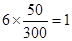 , 5分
, 5分
第2组的人数为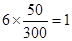 , 6分
, 6分
第3组的人数为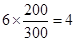 , 7分
, 7分
所以第1,2,3组分别抽取1人,1人,4人. 8分
(3)设第1组的1位同学为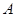 ,第2组的1位同学为
,第2组的1位同学为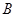 ,第3组的4位同学为
,第3组的4位同学为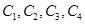 ,则从六位同学中抽两位同学有:
,则从六位同学中抽两位同学有: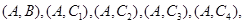
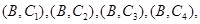
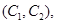
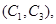
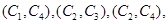
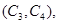 共
共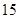 种可能. 10分
种可能. 10分
其中恰有1人年龄在第3组有8种可能, 12分
所以恰有1人年龄在第3组的概率为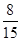 13分
13分
考点:1.频率分布直方图;2.分层抽样;3.随机事件的概率.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 年多于10人的概率.
年多于10人的概率.(2)根据这
 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值。
年的估计值。参考:用最小二乘法求线性回归方程系数公式

为预防H7N9病毒爆发,某生物技术公司研制出一种H7N9病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | 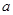 | 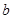 |
| 疫苗无效 | 77 | 90 | 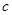 |
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取样本多少个?
(2)已知
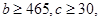 求通过测试的概率.
求通过测试的概率. 某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1~50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
(Ⅰ)观察乙抽取的样本数据,若从男同学中抽取两名,求两名男同学中恰有一名非优秀的概率.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
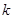 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
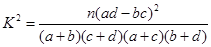 ,其中
,其中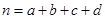 )
) 
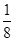 ,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。
,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。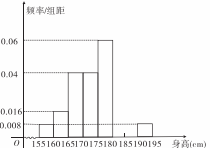
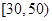 和
和 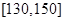 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s;