题目内容
函数y=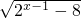
的定义域是________．
[4，+∞）
分析：根据函数有意义条件可得，2x-1-8≥0结合函数y=2x的单调性可求答案．
解答：根据函数有意义条件可得，2x-1-8≥0
即2x-1≥23
因为函数y=2x在R上单调递增
所以x-1≥3
所以x≥4
故答案为：[4，+∞）
点评：本题以函数的定义域的求解为载体，考查了指数函数的单调性的简单运用，属于基础试题．
分析：根据函数有意义条件可得，2x-1-8≥0结合函数y=2x的单调性可求答案．
解答：根据函数有意义条件可得，2x-1-8≥0
即2x-1≥23
因为函数y=2x在R上单调递增
所以x-1≥3
所以x≥4
故答案为：[4，+∞）
点评：本题以函数的定义域的求解为载体，考查了指数函数的单调性的简单运用，属于基础试题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
的定义域是_________.
的定义域是( )
的定义域是A，函数y=
（a＞0）在[0，2]上的值域为B．若A⊆B，求实数a的取值范围．
的定义域是 ．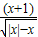
的定义域是 ．