题目内容
对于空间任一点O和不共线的三点A,B,C,有
=x
+y
+z
,则x+y+z=1是P,A,B,C四点共面的( )
| OP |
| OA |
| OB |
| OC |
分析:从共面向量定理出发,判断对于空间任意一点O和不共线三点A,B,C,点P满足
=x
+y
+z
,且x+y+z=1向量
,
,
共面,得到P,A,B,C四点共面,可以是充分条件;再通过举出反例得出反面不成立,即可得出答案.
| OP |
| OA |
| OB |
| OC |
| AP |
| AB |
| AC |
解答:解:若x+y+z=1,则
=(1-y-z)
+y
+z
,即
=y
+z
,
由共面定理可知向量
,
,
共面,所以P,A,B,C四点共面;
反之,若P,A,B,C四点共面,当O与四个点中的一个(比如A点)重合时,
=
,x可取任意值,不一定有x+y+z=1,
则x+y+z=1是P,A,B,C四点共面的充分不必要条件.
故选B.
| OP |
| OA |
| OB |
| OC |
| AP |
| AB |
| AC |
由共面定理可知向量
| AP |
| AB |
| AC |
反之,若P,A,B,C四点共面,当O与四个点中的一个(比如A点)重合时,
| OA |
| 0 |
则x+y+z=1是P,A,B,C四点共面的充分不必要条件.
故选B.
点评:本题考查共线向量与共面向量定理,考查充要条件的判断,考查计算能力,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
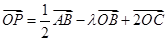 ,则λ=_____________.
,则λ=_____________. =x
=x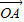 +y
+y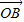 +z
+z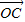 ,则x+y+z=1是P,A,B,C四点共面的( )
,则x+y+z=1是P,A,B,C四点共面的( )