题目内容
（04年全国卷Ⅱ）(12分)
已知锐角三角形ABC中，sin(A＋B)＝
，sin(A－B)＝
．
(Ⅰ)求证：tanA＝2tanB；
(Ⅱ)设AB＝3，求AB边上的高．
17．解析：(I)证明：∵sin(A+B)=
,sin(A-B)=
∴
，∴
.
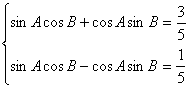
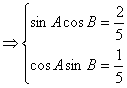
(II)解：∵
<A+B<π, 
, ∴
, 
即
,将代入上式并整理得
解得
,因为B为锐角，所以
,∴ =2+
设AB上的高为CD，则AB=AD+DB=
，由AB=3得CD=2+
故AB边上的高为2+
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
的所有正数
从小到大排成数列
}为等比数列；
是数列{
}的前n项和，求
（ ）
D．－
的图象（ ）
的图象关于y轴对称 B．与
的图象关于y轴对称 D．与