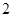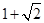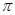题目内容
设向量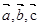 ,满足
,满足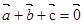 ,且
,且 ,
, ,则
,则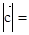 ( ).
( ).
| A.1 | B. | C.2 | D.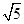 |
D
解析试题分析:根据题意,由于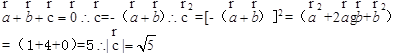
故可知答案D.
考点:向量的数量积
点评:本题考查向量的数量积和向量的模长公式,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,D为等腰三角形ABC底边AB的中点,则下列等式恒成立的是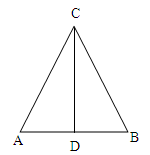
A. | B.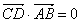 |
C.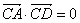 | D.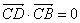 |
设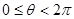 ,已知两个向量
,已知两个向量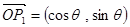 ,
,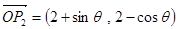 ,则向量
,则向量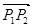 长度的最大值是( )
长度的最大值是( )
A.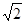 | B.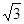 | C.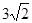 | D.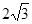 |
平面向量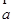 与
与 的夹角为
的夹角为 ,
, ,则
,则 =( )
=( )
A. | B.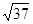 | C.7 | D.3 |
已知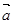 与
与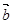 的夹角为
的夹角为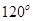 ,
,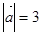 ,
,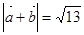 ,则
,则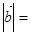 ( )
( )
| A.5 | B.4 | C.3 | D.1 |
已知向量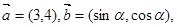 且
且 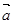 //
//  ,则
,则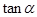 =( )
=( )
A.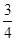 | B.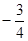 | C.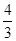 | D.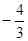 |
已知 为坐标原点,
为坐标原点,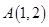 ,点
,点 的坐标
的坐标 满足约束条件
满足约束条件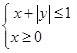 ,则
,则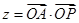 的最大值为
的最大值为
A. | B.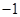 | C.1 | D.2 |
设向量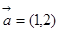 ,
,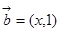 ,当向量
,当向量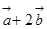 与
与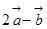 平行时,则
平行时,则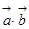 等于
等于
| A.2 | B.1 | C.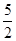 | D.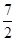 |
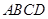 的顶点
的顶点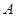 ,
,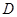 分别在
分别在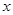 轴、
轴、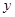 轴正半轴上移动,则
轴正半轴上移动,则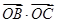 的最大值是( )
的最大值是( )