题目内容
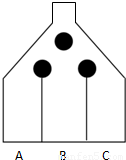
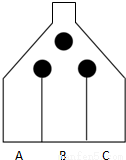
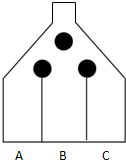 现有一游戏装置如图,小球从最上方入口处投入,每次遇到黑色障碍物,等可能地向左,右两边落下.游戏规则为:若小球最终落入A槽,得10张奖票;若落入B槽,得5张奖票;若落入C槽,得重投一次的机会,但投球的总次数不超过3次.
现有一游戏装置如图,小球从最上方入口处投入,每次遇到黑色障碍物,等可能地向左,右两边落下.游戏规则为:若小球最终落入A槽,得10张奖票;若落入B槽,得5张奖票;若落入C槽,得重投一次的机会,但投球的总次数不超过3次.(1)求投球一次,小球落入B槽的概率;
(2)设玩一次游戏能获得的奖票数为随机变量ξ,并求ξ的分布列及数学期望.
分析:(1)小球落入B袋中包含两种情形当且仅当小球先向左再向右或者先向右再向左,然后求出两种情形的概率和即可;
(2)分别计算出小球落入A槽,落入B槽,落入C槽的概率,根据题意可得ξ的取值为0、5、10,列出分布列,根据数学期望的公式解之即可.
(2)分别计算出小球落入A槽,落入B槽,落入C槽的概率,根据题意可得ξ的取值为0、5、10,列出分布列,根据数学期望的公式解之即可.
解答:解:(1)由题意可知:若投一次小球,则落入B槽的概率为(
)2+(
)2=
.
(2)落入A槽的概率为(
)2=
,落入B槽的概率为
,落入C槽的概率为(
)2=
,
由题意可得:ξ可能取的数值为0,5,10…(5分),
p(ξ=0)=(
)3=
,…(6分)
p(ξ=5)=
+
•
+
•(
)2=
,…(8分)
p(ξ=10)=
+
•
+
•(
)2=
,…(10分)
所以ξ的分布列为:
则ξ的数学期望为:Eξ=0×
+5×
+10×
=
.…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)落入A槽的概率为(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由题意可得:ξ可能取的数值为0,5,10…(5分),
p(ξ=0)=(
| 1 |
| 4 |
| 1 |
| 64 |
p(ξ=5)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 21 |
| 32 |
p(ξ=10)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 21 |
| 64 |
所以ξ的分布列为:
| ξ | 0 | 5 | 10 | ||||||
| p |
|
|
|
| 1 |
| 64 |
| 21 |
| 32 |
| 21 |
| 64 |
| 105 |
| 16 |
点评:本题考查相互独立事件同时发生的概率,考查离散型随机变量的分布列和期望,是一个概率的综合题,解题时注意两问之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
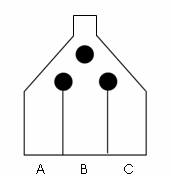
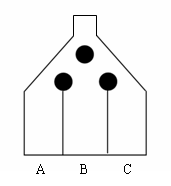 游戏规则为:若小球最终落入A槽,得10张奖票;若落入B槽,得5张奖票;若落入C槽,得重投一次的机会,但投球的总次数不超过3次。
游戏规则为:若小球最终落入A槽,得10张奖票;若落入B槽,得5张奖票;若落入C槽,得重投一次的机会,但投球的总次数不超过3次。