题目内容
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的25%.现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:1.002500≈2.7)
分析:由题意,符合公司要求的模型只需满足:当x∈[10,1000]时,①函数为增函数;②函数的最大值不超过5;③y≤x•25%,然后一一验证即可.
解答:解:函数f1(x)=0.25x,f3(x)=1.002x在[10,1000]内单调递增,且f1(1000)=250,f3(1000)=(1+0.002)1000=[(1+0.002)500]2≈2.72=7.29,两者都大于5万元,因而第一、三两个模拟函数显然不符合公司要求.…(3分)
而对于函数f2(x)=log7x+1,函数在[10,1000]上也是单调递增的,而且f2(1000)=log71000+1<log774+1=5,因而符合第一个要求;…(6分)
下面再考虑
=
≤0.25是否在[10,1000]上恒成立.
令f(x)=log7x-
x+1,x∈[10,1000],
则f′(x)=
log7e-
≤
log7e-
<
-
<0,
从而fmax(x)=f(10)=log710-
=
(log343100-1)<0,则f(x)<0.
即
=
≤0.25成立,因而符合公司的第二个要求.
综上所述,只有模型y=log7x+1能符合公司要求.…(12分)
而对于函数f2(x)=log7x+1,函数在[10,1000]上也是单调递增的,而且f2(1000)=log71000+1<log774+1=5,因而符合第一个要求;…(6分)
下面再考虑
| y |
| x |
| log7x+1 |
| x |
令f(x)=log7x-
| 1 |
| 4 |
则f′(x)=
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 4 |
从而fmax(x)=f(10)=log710-
| 3 |
| 2 |
| 3 |
| 2 |
即
| y |
| x |
| log7x+1 |
| x |
综上所述,只有模型y=log7x+1能符合公司要求.…(12分)
点评:本题以实际问题为载体,考查函数模型的构建,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
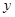 (单位:万元)随销售利润
(单位:万元)随销售利润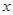 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的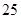 %.现有三个奖励模型:
%.现有三个奖励模型: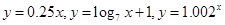 ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: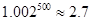 )
)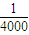 x2
x2