题目内容
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合如右图所示.将矩形折叠,使A点落在线段DC上.
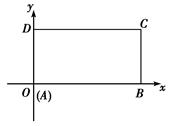
若折痕所在直线的斜率为k,试写出折痕所在直线的方程.

若折痕所在直线的斜率为k,试写出折痕所在直线的方程.
①当k=0时,此时A点与D点重合,
折痕所在的直线方程y=,
②当k≠0时,将矩形折叠后A点落在线段CD上的点为
G(a,1),所以A与G关于折痕所在的直线对称,
有kOG·k=-1,k=-1⇒a=-k,
故G点坐标为G(-k,1),从而折痕所在的直线与OG的交点坐标(线段OG的中点)为M,
折痕所在的直线方程y-=k,
即y=kx++
由①②得折痕所在的直线方程为:
k=0时,y=;k≠0时y=kx++.
折痕所在的直线方程y=,
②当k≠0时,将矩形折叠后A点落在线段CD上的点为
G(a,1),所以A与G关于折痕所在的直线对称,
有kOG·k=-1,k=-1⇒a=-k,
故G点坐标为G(-k,1),从而折痕所在的直线与OG的交点坐标(线段OG的中点)为M,
折痕所在的直线方程y-=k,
即y=kx++
由①②得折痕所在的直线方程为:
k=0时,y=;k≠0时y=kx++.
略

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
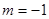 是直线
是直线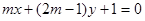 和直线
和直线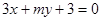 垂直的
垂直的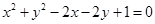 上的点到直线
上的点到直线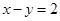 的距离最大值是( )
的距离最大值是( )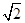
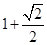
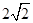

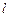 经过点
经过点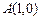 和
和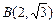
 ,则直线
,则直线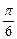
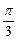


 ,“供给—价格”函数的图像为直线
,“供给—价格”函数的图像为直线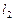 ,它们的斜率分别为
,它们的斜率分别为 ,
, 为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点
为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点


 可取任意实数
可取任意实数



 平行,求
平行,求 的值。
的值。