题目内容
已知a为正的常数,若不等式 对一切非负实数x恒成立,则a的最大值为________.
对一切非负实数x恒成立,则a的最大值为________.
8
分析:依题意,可将a分离出来,构造函数,f(x)=4(1+ +
+ )(x≥0),利用该函数的单调递增的性质求其最小值,即可求得a的最大值.
)(x≥0),利用该函数的单调递增的性质求其最小值,即可求得a的最大值.
解答:∵a>0,x≥0, ≥1+
≥1+ -
-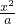 ,
,
∴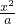 ≥1+
≥1+ -
- =
=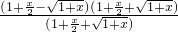 =
=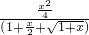 =
= ,
,
∴0<a≤4(1+ +
+ )对一切非负实数x恒成立.
)对一切非负实数x恒成立.
令f(x)=4(1+ +
+ )(x≥0),则0<a≤f(x)min.
)(x≥0),则0<a≤f(x)min.
∵f′(x)=4( +
+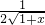 )>0,
)>0,
∴f(x)=4(1+ +
+ )(x≥0)在[0,+∞)上单调递增,
)(x≥0)在[0,+∞)上单调递增,
∴f(x)min=f(0)=8.
∴0<a≤8.
故a的最大值为8.
故答案为:8.
点评:本题考查函数恒成立问题,分离参数a,构造函数f(x)=4(1+ +
+ )(x>0)是关键,也是难点,考查创新思维与转化思想,属于难题.
)(x>0)是关键,也是难点,考查创新思维与转化思想,属于难题.
分析:依题意,可将a分离出来,构造函数,f(x)=4(1+
 +
+ )(x≥0),利用该函数的单调递增的性质求其最小值,即可求得a的最大值.
)(x≥0),利用该函数的单调递增的性质求其最小值,即可求得a的最大值.解答:∵a>0,x≥0,
 ≥1+
≥1+ -
-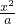 ,
,∴
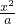 ≥1+
≥1+ -
- =
=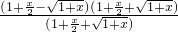 =
=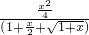 =
= ,
,∴0<a≤4(1+
 +
+ )对一切非负实数x恒成立.
)对一切非负实数x恒成立.令f(x)=4(1+
 +
+ )(x≥0),则0<a≤f(x)min.
)(x≥0),则0<a≤f(x)min.∵f′(x)=4(
 +
+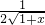 )>0,
)>0,∴f(x)=4(1+
 +
+ )(x≥0)在[0,+∞)上单调递增,
)(x≥0)在[0,+∞)上单调递增,∴f(x)min=f(0)=8.
∴0<a≤8.
故a的最大值为8.
故答案为:8.
点评:本题考查函数恒成立问题,分离参数a,构造函数f(x)=4(1+
 +
+ )(x>0)是关键,也是难点,考查创新思维与转化思想,属于难题.
)(x>0)是关键,也是难点,考查创新思维与转化思想,属于难题. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,求函数g(x)在区间[1,e]上的最小值.
,求函数g(x)在区间[1,e]上的最小值. 对一切非负实数x恒成立,则a的最大值为 .
对一切非负实数x恒成立,则a的最大值为 .