题目内容
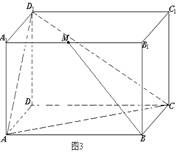
如图3-1.已知![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 和棱
和棱![]() 的中点.
的中点.
(Ⅰ)试判断四边形![]() 的形状;
的形状;
(Ⅱ)求证:平面![]() 平面
平面![]() .
.

(Ⅰ)菱形(Ⅱ)证明见解析
解析:
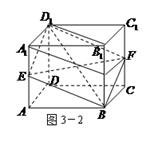
(Ⅰ)如图3-2,取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() .
.
 ∵
∵![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
∴![]() ,
,
在正方体![]() 中,有
中,有
![]() , ∴
, ∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
故![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
又![]() ≌
≌![]() ,
,
∴![]() ,
,
故四边形![]() 为菱形.
为菱形.
(Ⅱ)连结![]() 、
、![]() 、
、![]() . ∵四边形
. ∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
在正方体![]() 中,有
中,有
![]() ,
,
![]()
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]()

练习册系列答案
相关题目
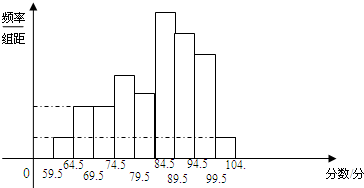 为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则
为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则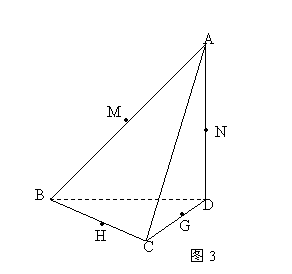



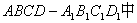 ,
,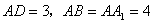 ,M是
,M是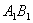 的中点.
的中点.
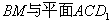 所成的角;
所成的角; 的距离.
的距离.