题目内容
已知奇函数f(x)在[-1,0]上为单调递减函数,又a,b为锐角三角形两内角,下列结论正确的是
| A.f(cosa)> f(cosb) | B.f(sina)> f(sinb) |
| C.f(sina)> f(cosb) | D.f(sina)<f(cosb) |
D
试题分析:∵奇函数y=f(x)在[-1,0]上为单调递减函数,∴f(x)在[0,1]上为单调递减函数,∴f(x)在[-1,1]上为单调递减函数。
又α、β为锐角三角形的两内角
∴α+β>
 ,∴α>
,∴α> -β
-β∴sinα>sin(
 -β)=cosβ>0
-β)=cosβ>0∴f(sinα)<f(cosβ)
故选D。
点评:小综合题,利用奇函数的性质确定f(x)在[-1,1]上为单调递减函数。利用诱导公式得到sinα>sin(
 -β)=cosβ>0 。
-β)=cosβ>0 。
练习册系列答案
相关题目
 ,且
,且 ,则
,则 的值为 。
的值为 。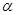 为第三象限角,
为第三象限角,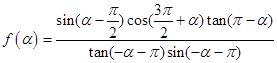 .
.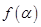 (2)若
(2)若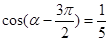 ,求
,求 的相邻两条对称轴之间的距离为 ( )
的相邻两条对称轴之间的距离为 ( )



 的值域是( )
的值域是( )



 ,
,
 ,
, ,
, ,若
,若 最小值为
最小值为 ,则
,则 的值为 。
的值为 。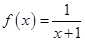 ,点
,点 为坐标原点,点
为坐标原点,点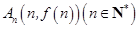 . 若记直线
. 若记直线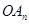 的倾斜角为
的倾斜角为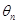 ,则
,则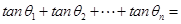




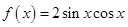
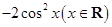 .
.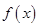 的最小正周期;
的最小正周期;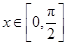 时,求函数
时,求函数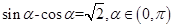 ,则
,则