题目内容
如图，从椭圆
＋
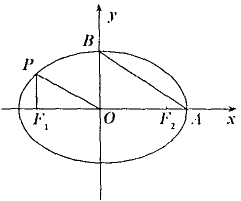
＝1(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP，|F1A|＝
＋
，求此椭圆方程．
答案：
解析：
解析：
|
热点分析 求出P点的坐标，利用kAB＝kOP或利用两直角三角形相似及|F1A|＝a＋c建立两个关系，再结合a2＝b2＋c2可得解． 解答 ∵AB∥OP，∠BAO＝∠POF1，PF1⊥x轴，∴Rt△ABO∽Rt△OPF1，得 ∴yP＝|F1P|＝ 评析 求椭圆的方程，先判断焦点的位置，若焦点位置不确定则进行讨论，还要善于利用椭圆的定义和性质结合图形建立关系式． |
＝
，
，而xP＝－c代椭圆方程得yP＝
，由
，得b＝c，∴a＝
c．而a＋c＝
＋
，解得b＝c＝
，∴a＝
，∴所求方程为
＋
＝1．
练习册系列答案
相关题目
的图像是以直线y＝x为轴，以坐标轴为渐近线的等轴双曲线，记作C．
的左、右准线分别为l1，l2，且分别交x轴于C，D两点，从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与交于点B，若AF⊥BF，且∠ABD＝75°，则椭圆的离心率等于________．
，求|BC|与|AD|的比值；
，△BDM和△ABN的面积分别为S1和S2．