题目内容
下面有5个命题:
①分针每小时旋转2π弧度; ②函数f(x)=
是奇函数;
③若
=x
+y
,且x+y=1,则A,B,C三点共线;
④在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
⑤在△ABC中,若sinA=sinB,则A=B.
其中,真命题的编号是
①分针每小时旋转2π弧度; ②函数f(x)=
| sinx |
| 1+cosx |
③若
| OA |
| OB |
| OC |
④在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
⑤在△ABC中,若sinA=sinB,则A=B.
其中,真命题的编号是
②③⑤
②③⑤
(写出所有真命题的编号)分析:①分针的旋转是顺时针方向,应为负角.
②按照奇函数定义判断即可.
③将已知转化成
=x
可知正确.
④转化成y=sinx-x零点个数问题.
⑤根据正弦定理易判断为真.
②按照奇函数定义判断即可.
③将已知转化成
| CA |
| CB |
④转化成y=sinx-x零点个数问题.
⑤根据正弦定理易判断为真.
解答:解:
①分针的旋转是顺时针方向,每小时旋转一周,应为每小时旋转-2π弧度.①假
②f(x)的定义域为:cosx≠-1,x≠kπ,k∈Z,且f(-x)═
=-
=-f(x).②真
③由已知,
=x
+(1-x)
=x(
-
) +
,
移向得,
-
=X(
-
),
=x
,
与
共线,
所以A,B,C三点共线,③真
④考察函f(x)=sinx-x,其导函数y′=cosx-1≤0,
∴f(x)在R上单调递减,且f(0)=0,
∴f(x)=sinx-x图象与轴只有一个交点.
∴f(x)=sinx与y=x 图象只有一个交点,④假
⑤在△ABC中,若sinA=sinB,由正弦定理,可得a=b,从而A=B.⑤真.
故答案为:②③⑤.
①分针的旋转是顺时针方向,每小时旋转一周,应为每小时旋转-2π弧度.①假
②f(x)的定义域为:cosx≠-1,x≠kπ,k∈Z,且f(-x)═
| sin(-x) |
| 1+cos(-x) |
| sinx |
| 1+cosx |
③由已知,
| OA |
| OB |
| OC |
| OB |
| OC |
| OC |
移向得,
| OA |
| OC |
| OB |
| OC |
| CA |
| CB |
| CA |
| CB |
所以A,B,C三点共线,③真
④考察函f(x)=sinx-x,其导函数y′=cosx-1≤0,
∴f(x)在R上单调递减,且f(0)=0,
∴f(x)=sinx-x图象与轴只有一个交点.
∴f(x)=sinx与y=x 图象只有一个交点,④假
⑤在△ABC中,若sinA=sinB,由正弦定理,可得a=b,从而A=B.⑤真.
故答案为:②③⑤.
点评:本题考查命题真假的判断,主要考查了角的概念的推广、函数的奇偶性、向量计算及共线、函数图象、正弦定理等知识,均为中学阶段基础而重要的知识.不可忽视基础知识在学习中的地位.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 弧度;
弧度; ,且
,且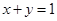 ,则
,则 三点共线;
三点共线; 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点; 是奇函数;
是奇函数; 中,若
中,若 ,则
,则 。
。 是奇函数;
是奇函数; ,且x+y=1,则A,B,C三点共线;
,且x+y=1,则A,B,C三点共线;