题目内容
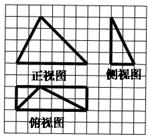
一个几何体的三视图如图,则该几何体的体积为( )
A. | B. | C. | D. |
D
解析试题分析:由三视图可知原几何体是一个底面为正方形的对角线为2四棱锥,四棱锥的高为1,.所以底面积为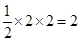 .所以四棱锥的体积为
.所以四棱锥的体积为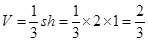 .故选D.本小题关键需要具备通过三视图构建直观图形的空间想象能力.
.故选D.本小题关键需要具备通过三视图构建直观图形的空间想象能力.
考点:1.三视图的知识.2.体积公式.3.空间想象能力.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
某三棱锥的三视图如图所示,该三棱锥的体积为( )
A. | B. | C. | D. |
某师傅需用合板制作一个工作台,工作台由主体和附属两部分组成,主体部分全封闭,附属部分是为了防止工件滑出台面而设置的三面护墙,其大致形状的三视图如图所示(单位长度: cm), 则按图中尺寸,做成的工作台用去的合板的面积为(制作过程合板的损耗和合板厚度忽略不计)( )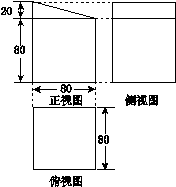
| A.40 000 cm2 | B.40 800 cm2 |
C.1600(22+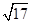 )cm2 )cm2 | D.41 600 cm2 |
如图,某几何体的正视图、侧视图、俯视图均为直角三角形,则这个几何体的表面中,直角三角形个数为( ).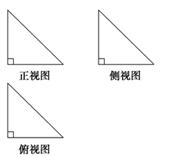
| A.1 | B.2 | C.3 | D.4 |
已知一个几何体的三视图如下图,则该几何体的体积为( ).
A.8- | B.8- |
C.4- | D.4- |
一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( ).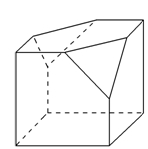
| A.7 | B. | C.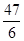 | D. |
 的底面是正三角形,各条侧棱均相等,
的底面是正三角形,各条侧棱均相等,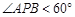 . 设点
. 设点 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,记
,记 ,
, 周长为
周长为 ,则
,则 的图象可能是( )
的图象可能是( )
 的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )
的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )