题目内容
已知函数
，设F(x)＝f(x)＋g(x)
(1)求F(x)的单调区间；
(2)若以y＝F(x)(x∈(0，2])图像上任意一点P(x0，y0)为切点的切线的斜率
恒成立，求实数a的最小值；
(3)若对所有的x∈[e，＋∞)都有
xf(x)≥ax－a成立，求实数a的取值范围．
答案：
解析：
解析：
|
(1) 因为 由 (2) 即 所以 (3)因为 则 因为当 所以 所以 |
． 2分
由
，所以
在
上单调递增；
，所以
上单调递减． 5分
恒成立， 7分
当
时取得最大值3．所以，
，
10分
，所以
，令
，
． 12分
，
，
，所以
，所以
． 15分
练习册系列答案
相关题目
，设f(x)的最大值、最小值分别为m，n，若m－n＜1，则正整数a的取值个数是
其中
是的f(x)的导函数。
的一切
的值， 都有
求实数ｘ的取值范围；
，当实数ｍ在什么范围内变化时，函数ｙ＝f(x)的图像与直线ｙ＝3只有一个公共点。
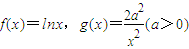，设F（x）=f（x）+g（x）．
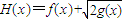，图象上任意一点P（x，y）为切点的切线的斜率k≤1恒成立，求实数a的最小值；
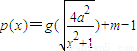的图象与q（x）=f（1+x2）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．