题目内容
曲线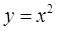 与直线
与直线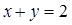 围成的图形的面积为( )
围成的图形的面积为( )
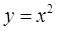 与直线
与直线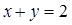 围成的图形的面积为( )
围成的图形的面积为( )A. | B. | C. | D. |
C
先根据题意画出区域,然后依据图形得到积分下限为-2,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解先根据题意画出图形,得到积分上限为1,积分下限为-2曲线y=x2与直线x+y=2围成的图形的面积为:
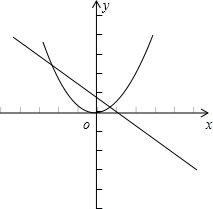
S=∫-21(2-x-x2)dx
而∫-21(2-x-x2)dx=(2x-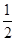 x2-
x2-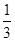 x3)|-21=
x3)|-21=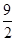
∴曲边梯形的面积是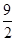
故选C.
解先根据题意画出图形,得到积分上限为1,积分下限为-2曲线y=x2与直线x+y=2围成的图形的面积为:
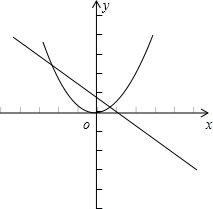
S=∫-21(2-x-x2)dx
而∫-21(2-x-x2)dx=(2x-
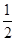 x2-
x2-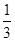 x3)|-21=
x3)|-21=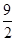
∴曲边梯形的面积是
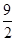
故选C.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
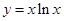 在点
在点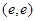 处的切线与直线
处的切线与直线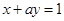 垂直,则实数
垂直,则实数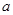 的值为
的值为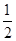
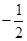
 +2
+2 +3
+3 =0,则直线AB与x轴的交点的横坐标为
=0,则直线AB与x轴的交点的横坐标为 

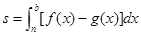 求出的是 ( )
求出的是 ( )
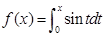 ,则
,则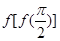 的值等于( )
的值等于( )



 =
=  ,若,
,若, ,则
,则 。
。 ,则
,则 的值是( )
的值是( )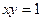 ,直线
,直线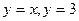 所围成的平面图形的面积为( )
所围成的平面图形的面积为( )


