题目内容
2.已知△OFQ的面积为S,且$\overrightarrow{OF}$•$\overrightarrow{FQ}$=1.(1)若$\frac{1}{2}$<S<2,向量$\overrightarrow{OF}$与$\overrightarrow{FQ}$的夹角为θ,求tanθ取值范围;
(2)设|$\overrightarrow{OF}$|=c(c≥2),S=$\frac{3}{4}$c,若以O为中心,F为焦点的椭圆经过点Q,当|$\overrightarrow{OQ}$|取最小值时,建立坐标系求此时椭圆的方程.
分析 (1)由题意知$|\begin{array}{l}{\overrightarrow{OF}}\end{array}||\begin{array}{l}{\overrightarrow{FQ}}\end{array}|=\frac{1}{cosθ}$,$S=\frac{1}{2}tanθ$,从而1<tanθ<4;
(2)以O为原点,OF所在直线为x轴建立直角坐标系,并设Q(m,n),则F(c,0),由题意知$\overrightarrow{OF}•\overrightarrow{FQ}=c(m-c)=1$,则$m=c+\frac{1}{c}$.由此知${|\begin{array}{l}{\overrightarrow{OQ}}\end{array}|}^{2}=(c+\frac{1}{c})^{2}+\frac{9}{4}$,由此入手,当$|\begin{array}{l}{\overrightarrow{OQ}}\end{array}|$取最小值时,能够求出椭圆的方程.
解答 解:(1)由题意知,$\overrightarrow{OF}•\overrightarrow{FQ}=|\begin{array}{l}{\overrightarrow{OF}}\end{array}||\begin{array}{l}{\overrightarrow{FQ}}\end{array}|cosθ=1$
所以$|\begin{array}{l}{\overrightarrow{OF}}\end{array}||\begin{array}{l}{\overrightarrow{FQ}}\end{array}|=\frac{1}{cosθ}$,
因为$S=\frac{1}{2}|\begin{array}{l}{\overrightarrow{OF}}\end{array}||\begin{array}{l}{\overrightarrow{FQ}}\end{array}|sin(π-θ)$=$\frac{1}{2}|\begin{array}{l}{\overrightarrow{OF}}\end{array}||\begin{array}{l}{\overrightarrow{FQ}}\end{array}|sinθ$,
所以$S=\frac{1}{2}tanθ$,
又$\frac{1}{2}$<S<2,
所以1<tanθ<4;
(2)以O为原点,OF所在直线为x轴建立直角坐标系,
并设Q(m,n),则F(c,0),
且$\left\{\begin{array}{l}{S=\frac{1}{2}cn}\\{S=\frac{3}{4}c}\end{array}\right.$,故$n=\frac{3}{2}$.
因为$\overrightarrow{OF}=(c,0)$,$\overrightarrow{FQ}=(m-c,n)$,
所以$\overrightarrow{OF}•\overrightarrow{FQ}=c(m-c)=1$,
则$m=c+\frac{1}{c}$,故$Q(c+\frac{1}{c},\frac{3}{2})$.
从而${|\begin{array}{l}{\overrightarrow{OQ}}\end{array}|}^{2}=(c+\frac{1}{c})^{2}+\frac{9}{4}$.
又c≥2,
故当c=2时,$|\begin{array}{l}{\overrightarrow{OQ}}\end{array}|$最小,此时$Q(\frac{5}{2},\frac{3}{2})$.
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\\;\\;(a>b>0)$,
则有$\left\{\begin{array}{l}{{c}^{2}=4={a}^{2}-{b}^{2}}\\{\frac{(\frac{5}{2})^{2}}{{a}^{2}}+\frac{(\frac{3}{2})^{2}}{{b}^{2}}=1}\end{array}\right.$
解得a2=10,b2=6,
故椭圆的方程为:$\frac{{x}^{2}}{10}+\frac{{y}^{2}}{6}=1$.
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意积累解题方法.

 阅读快车系列答案
阅读快车系列答案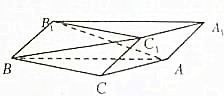 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2,
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2,