题目内容
(08年雅礼中学一模理)(13分) 已知点![]()
(Ⅰ)求f(x)的定义域;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:数列{an}前n项和![]()
解析:(Ⅰ)由![]()
![]()
故x>0或x≤-1
f(x)定义域为![]() …………………………(4分)
…………………………(4分)
(Ⅱ)![]()

下面使用数学归纳法证明:![]()
①在n=1时,a1=1,![]() <a1<2,则n=1时(*)式成立.
<a1<2,则n=1时(*)式成立.
②假设n=k时![]() 成立,
成立,
由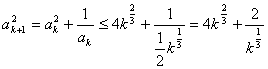
要证明:
只需![]()
只需(2k+1)3≤8k(k+1)2
只需1≤4k2+2k
而4k2+2k≥1在k≥1时恒成立.
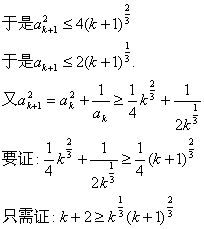
只需证:4k2+11k+8>0,而4k2+11k+8>0在k≥1时恒成立.
于是:![]()
因此![]() 得证.
得证.
综合①②可知(*)式得证.从而原不等式成立. ………………9分
(Ⅲ)要证明:![]()
由(2)可知只需证:
![]() …………(**)
…………(**)
下面用分析法证明:(**)式成立。
要使(**)成立,只需证:![]()
即只需证:(3n-2)3n>(3n-1)3(n-1)
只需证:2n>1
而2n>1在n≥1时显然成立.故(**)式得证:
于是由(**)式可知有:
![]()
因此有:![]()
![]() ……………………………………(13分)
……………………………………(13分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目