题目内容
已知函数f(x)=aln x-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2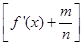 (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: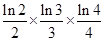 ×…×
×…×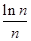 <
<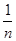 (n≥2,n∈N*)
(n≥2,n∈N*)
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2
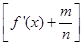 (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;(3)求证:
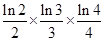 ×…×
×…×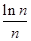 <
<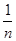 (n≥2,n∈N*)
(n≥2,n∈N*)(1)单调增区间为(1,+∞),减区间为(0,1).(2)不是,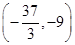 (3)见解析
(3)见解析
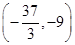 (3)见解析
(3)见解析(1)解 当a=-1时,f′(x)=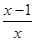 (x>0)
(x>0)
令f′(x)>0,得x∈(1,+∞);
令f′(x)<0,得x∈(0,1).
∴函数f(x)的单调增区间为(1,+∞),减区间为(0,1).
(2)解 ∵f′(x)= (x>0),∴f′(2)=-
(x>0),∴f′(2)=-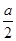 =1得a=-2,∴f(x)=-2ln x+2x-3,g(x)=x3+
=1得a=-2,∴f(x)=-2ln x+2x-3,g(x)=x3+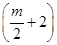 x2-2x,∴g′(x)=3x2+(m+4)x-2,∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴
x2-2x,∴g′(x)=3x2+(m+4)x-2,∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴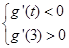
由题意知:对于任意的t∈[1,2],g′t<0恒成立,
所以,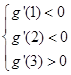 ∴-
∴-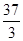 <m<-9.
<m<-9.
故m的取值范围是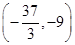 .
.
(3)证明 由(1)知当x∈(1,+∞)时f(x)>f(1),即-ln x+x-1>0,∴0<ln x<x-1对一切x∈(1,+∞)成立.
∵n≥2,n∈N*,则有0<ln n<n-1,∴0< .
.
∴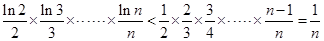 (n≥2,n∈N*).
(n≥2,n∈N*).
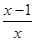 (x>0)
(x>0)令f′(x)>0,得x∈(1,+∞);
令f′(x)<0,得x∈(0,1).
∴函数f(x)的单调增区间为(1,+∞),减区间为(0,1).
(2)解 ∵f′(x)=
 (x>0),∴f′(2)=-
(x>0),∴f′(2)=-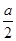 =1得a=-2,∴f(x)=-2ln x+2x-3,g(x)=x3+
=1得a=-2,∴f(x)=-2ln x+2x-3,g(x)=x3+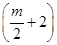 x2-2x,∴g′(x)=3x2+(m+4)x-2,∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴
x2-2x,∴g′(x)=3x2+(m+4)x-2,∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴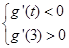
由题意知:对于任意的t∈[1,2],g′t<0恒成立,
所以,
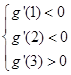 ∴-
∴-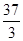 <m<-9.
<m<-9.故m的取值范围是
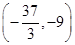 .
.(3)证明 由(1)知当x∈(1,+∞)时f(x)>f(1),即-ln x+x-1>0,∴0<ln x<x-1对一切x∈(1,+∞)成立.
∵n≥2,n∈N*,则有0<ln n<n-1,∴0<
 .
.∴
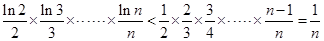 (n≥2,n∈N*).
(n≥2,n∈N*).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在
在 处存在极值.
处存在极值.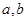 的值;
的值;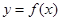 的图像上存在两点A,B使得
的图像上存在两点A,B使得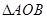 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在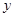 轴上,求实数
轴上,求实数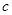 的取值范围;
的取值范围;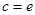 时,讨论关于
时,讨论关于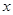 的方程
的方程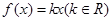 的实根个数.
的实根个数.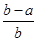 <ln
<ln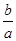 <
<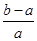 ,其中0<a<b;
,其中0<a<b;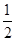 + +
+ +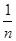 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).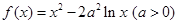 .
.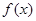 的单调区间;
的单调区间;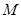 ,求证:
,求证: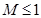 .
.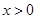 ,函数
,函数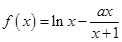 .
.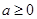 时,讨论函数
时,讨论函数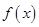 的单调性;
的单调性;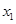 和
和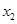 )时,求证:
)时,求证: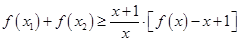 .
.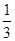 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).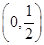 上不存在极值点,求a的取值范围.
上不存在极值点,求a的取值范围.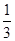 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.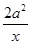 +x(a≠0),
+x(a≠0),