题目内容
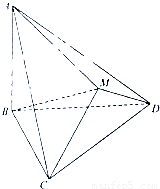
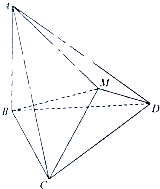 如图△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2| 3 |
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
分析:(1)取CD的中点,连接OB,OM,则OB⊥CD,OM⊥CD,又平面MCD⊥平面BCD,则MO⊥平面BCD,故MO∥AB,A,B,O,M共面,延长AM,BO相交于E,则∠AEB就是AM与平面BCD所成的角,由此能求出点A到平面MBC的距离.
(2)CE是平面ACM与平面BCD的交线,由(1)知,O是BE的中点,则BCED是菱形,作BF⊥EC于F,连接AF,∠AFB是二面角A-EC-B的平面角,由此能求出平面ACM与平面BCD所成二面角的正弦值.
(2)CE是平面ACM与平面BCD的交线,由(1)知,O是BE的中点,则BCED是菱形,作BF⊥EC于F,连接AF,∠AFB是二面角A-EC-B的平面角,由此能求出平面ACM与平面BCD所成二面角的正弦值.
解答: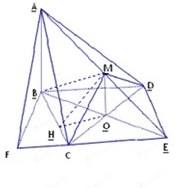 解:(1)取CD的中点,连接OB,OM,则OB⊥CD,OM⊥CD,
解:(1)取CD的中点,连接OB,OM,则OB⊥CD,OM⊥CD,
又平面MCD⊥平面BCD,
则MO⊥平面BCD,
∴MO∥AB,A,B,O,M共面,
延长AM,BO相交于E,则∠AEB就是AM与平面BCD所成的角,
OB=MO=
,
MO∥AB,MO∥面ABC,
M,O到平面 ABC的距离相等,作OH⊥BC于H,
连接MH,则MH⊥BC,
∴OH=OC•sin60°=
,MH=
,
∵VA-MBC=VM-ABC,
∴d=
.
(2)CE是平面ACM与平面BCD的交线,
由(1)知,O是BE的中点,则BCED是菱形,
作BF⊥EC于F,连接AF,∠AFB是二面角A-EC-B的平面角,设为θ,
∵∠BCE=120°,∴∠BCF=60°,
BF=BC•sin60°=
,
tanθ=
=2,sinθ=
,
所以平面ACM与平面BCD所成二面角的正弦值为
.
 解:(1)取CD的中点,连接OB,OM,则OB⊥CD,OM⊥CD,
解:(1)取CD的中点,连接OB,OM,则OB⊥CD,OM⊥CD,又平面MCD⊥平面BCD,
则MO⊥平面BCD,
∴MO∥AB,A,B,O,M共面,
延长AM,BO相交于E,则∠AEB就是AM与平面BCD所成的角,
OB=MO=
| 3 |
MO∥AB,MO∥面ABC,
M,O到平面 ABC的距离相等,作OH⊥BC于H,
连接MH,则MH⊥BC,
∴OH=OC•sin60°=
| ||
| 2 |
| ||
| 2 |
∵VA-MBC=VM-ABC,
∴d=
2
| ||
| 5 |
(2)CE是平面ACM与平面BCD的交线,
由(1)知,O是BE的中点,则BCED是菱形,
作BF⊥EC于F,连接AF,∠AFB是二面角A-EC-B的平面角,设为θ,
∵∠BCE=120°,∴∠BCF=60°,
BF=BC•sin60°=
| 3 |
tanθ=
| AB |
| BF |
2
| ||
| 5 |
所以平面ACM与平面BCD所成二面角的正弦值为
2
| ||
| 5 |
点评:本题考查点到平面的距离的求法,考查二面角的正弦值的求法.解题时要认真审题,注意合理地化空间问题为平面问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
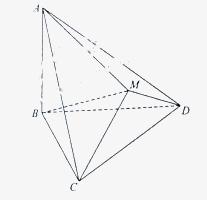 求点A到平面MBC的距离;
求点A到平面MBC的距离; 平面BCD,AB
平面BCD,AB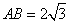 。
。 如图△BCD与△MCD都是边长为2的正三角形,平面MCD
如图△BCD与△MCD都是边长为2的正三角形,平面MCD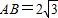 .
.