Question

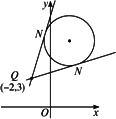
已知圆C：x²＋y²－4x－14y＋45＝0及点Q(－2，3)．

(1)若点P(m，m＋1)在圆C上，求PQ的斜率；

(2)若点M是圆C上任一点，则|MQ|的最大值、最小值分别是多少？

(3)若N(a，b)满足关系：a²＋b²－4a－14b＋45＝0，求的最大值．

Answer 1

答案：
解析：

解：(1)由于P(m，m＋1)在圆C上，所以有m2＋(m＋1)2－4m－14(m＋1)＋45＝0，解之，得m＝4，∴P(4，5)，从而kPQ＝． 　　(2)圆C的方程变为(x－2)2＋(y－7)2＝8．由于Q(－2，3)在圆C外部，且，如图，由平面几何知识可知|MQ|max＝|QC|＋r＝，|MQ|min＝|QC|－r＝． 　　(3)由N(a，b)满足的条件可知，N(a，b)在圆C上．又表示N(a，b)与Q(－2，3)两点连线的斜率．由图可知，t的最大值为过Q(－2，3)的圆C的两切线之一的斜率．设切线方程为y－3＝k(x＋2)，由圆心C(2，7)到其距离为，知k＝2±．所以tmax＝2＋． 　　思路解析：(1)将P点代入圆C的方程，可得出m的值． 　　(2)运用数形结合考虑，记圆心为C，则|MQ|max＝|QC|＋r，|MQ|min＝|QC|－r． 　　(3)考虑到具有几何意义，即表示圆C上的动点(a，b)与定点(－2，3)连线的斜率，故可用数形结合的方法．