题目内容
已知 ,解关于
,解关于 的不等式
的不等式 .
.
(1)当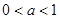 时,原不等式的解集为
时,原不等式的解集为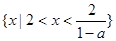 ,当
,当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当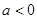 时,原不等式的解集为
时,原不等式的解集为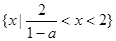 .
.
解析试题分析:(1)解决与之相关的问题时,可利用函数与方程的思想、化归的思想将问题转化,结合二次函数的图象来解决;(2)把分式不等式转化成整式不等式,注意看清分子、分母的符号;(3)解含参数的一元二次不等式分类讨论的依据:一是二次项中若含有参数应讨论是小于0,等于0,还是大于0,然后将不等式转化为二次项系数为正的形式,二是当不等式对应的方程的根个数不确定时,讨论判别式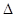 与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(4)讨论时注意找临界条件.
与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(4)讨论时注意找临界条件.
试题解析:解:不等式 可化为
可化为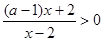
∵ ,∴
,∴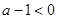 ,则原不等式可化为
,则原不等式可化为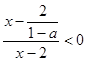
故当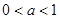 时,原不等式的解集为
时,原不等式的解集为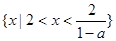 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当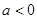 时,原不等式的解集为
时,原不等式的解集为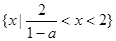 .
.
考点:分类讨论解不等式.

练习册系列答案
相关题目
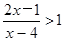 的解集是 .
的解集是 .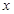 的不等式
的不等式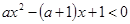
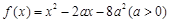 ,记不等式
,记不等式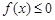 的解集为
的解集为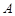 .
.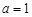 时,求集合
时,求集合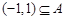 ,求实数
,求实数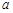 的取值范围.
的取值范围.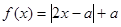 .
.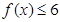 的解集为
的解集为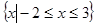 ,求实数a的值;(5分)
,求实数a的值;(5分)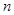 使
使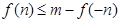 成立,求实数
成立,求实数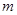 的取值范围.(5分)
的取值范围.(5分)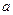 使得不等式
使得不等式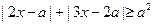 对任意实数
对任意实数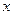 恒成立,则满足条件的
恒成立,则满足条件的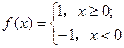 ,则不等式
,则不等式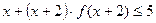 的解集是__________
的解集是__________