题目内容
16.已知集合X={x1,x2,…xn}(n∈N*,n≥3),若数列{xn}是等差数列,记集合P(X)={x|x=xi+xj,xi,xj?X,1≤i<j≤n,i,j∈N*}的元素个数为|P(X)|,则|P(X)|关于n的表达式为2n-3.分析 利用特殊化思想,取特殊的等差数列进行计算,结合类比推理可得|P(X)|=2n-3.
解答 解:∵集合X={a1,a2,…,an}(n∈N*,n≥3),定义集合P(X)={x|x=xi+xj,xi,xj∈X,1≤i<j≤n,i,j∈N*},
∴取特殊的等差数列进行计算,
取X={1,2,3,…,n},则|P(X)|={3,4,5,…,2n-1},
∵(2n-1)-3+1=2n-3,
∴P(X)=中共2n-3个元素,
利用类比推理可得
若a1,a2,…,an是公差大于零的等差数列,则|P(X)|=2n-3.
故答案为:2n-3.
点评 本题考查集合与元素的位置关系和数列的综合应用,综合性较强,解题时注意特殊化思想和转化思想的运用,解题时要认真审题,仔细解答,避免错误,属基础题.

练习册系列答案
相关题目
1.把正整数1,2,3,4,5,6,…按某种规律填入下表:
按照这种规律继续填写,那么2015出现在( )
| 2 | 6 | 10 | 14 | ||||||||
| 1 | 4 | 5 | 8 | 9 | 12 | 13 | …. | ||||
| 3 | 7 | 11 | 15 |
| A. | 第1行第1510列 | B. | 第3行第1510列 | C. | 第2行第1511列 | D. | 第3行第1511列 |
8.某单位为了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温:
由表中数据得线性方程$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x中$\widehat{b}$=-2,据此预测当天气温为5℃时,用电量的度数约为( )
| 气温(℃) | 14 | 12 | 8 | 6 |
| 用电量(度) | 22 | 26 | 34 | 38 |
| A. | 60 | B. | 50 | C. | 40 | D. | 30 |
5.某程序框图如图所示,若输出的S=41,则判断框内应填( )


| A. | k>4? | B. | k>5? | C. | k>6? | D. | k>7? |
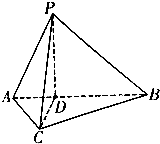 如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°.
如图所示,三棱锥P-ABC中,点D为线段AB上一点,AC⊥BC,PD⊥平面ABC,AD=$\frac{1}{2}$DB,PD=BD,∠ABC=30°. 如图所示,已知D、E、F分别是△ABC的边BC、CA、AB的中点,P是△ABC内任意一点,求证:$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$.
如图所示,已知D、E、F分别是△ABC的边BC、CA、AB的中点,P是△ABC内任意一点,求证:$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$.