题目内容
某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,1997年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.(1)若以1997年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?
(2)试估算2005年底该乡能否达到小康水平?为什么?
【答案】分析:(1)以1997年为第一年,根据甲企业以1.5倍的速度递增,而乙企业则为上一年利润的 ,则第n年该乡从这两家企业获得的利润为
,则第n年该乡从这两家企业获得的利润为 ,利用基本不等式可求两个企业获得利润最少的一年,从而可求还需另筹资金1040万元可解决温饱问题.
,利用基本不等式可求两个企业获得利润最少的一年,从而可求还需另筹资金1040万元可解决温饱问题.
(2)2005年为第9年,该年可从两个企业获得利润 ,利用基本不等式可知y9>8100
,利用基本不等式可知y9>8100
,从而可知该乡到2005年底可以达到小康水平.
解答:解:(1)若以1997年为第一年,则
∵甲企业以1.5倍的速度递增,而乙企业则为上一年利润的
∴第n年该乡从这两家企业获得的利润为
∴yn= =2×80×6=960
=2×80×6=960
当且仅当 ,即n=2时,等号成立,
,即n=2时,等号成立,
所以第二年(1998年)上交利润最少,利润为960万元.
由2000-960=1040(万元)知:还需另筹资金1040万元可解决温饱问题.
(2)2005年为第9年,该年可从两个企业获得利润
 >20×81×5=8100
>20×81×5=8100
所以该乡到2005年底可以达到小康水平.
点评:本题考查的重点是解决实际问题,解题的关键是构建函数模型,利用基本不等式解决最值问题,属于中档题.
 ,则第n年该乡从这两家企业获得的利润为
,则第n年该乡从这两家企业获得的利润为 ,利用基本不等式可求两个企业获得利润最少的一年,从而可求还需另筹资金1040万元可解决温饱问题.
,利用基本不等式可求两个企业获得利润最少的一年,从而可求还需另筹资金1040万元可解决温饱问题.(2)2005年为第9年,该年可从两个企业获得利润
 ,利用基本不等式可知y9>8100
,利用基本不等式可知y9>8100,从而可知该乡到2005年底可以达到小康水平.
解答:解:(1)若以1997年为第一年,则
∵甲企业以1.5倍的速度递增,而乙企业则为上一年利润的

∴第n年该乡从这两家企业获得的利润为

∴yn=
 =2×80×6=960
=2×80×6=960当且仅当
 ,即n=2时,等号成立,
,即n=2时,等号成立,所以第二年(1998年)上交利润最少,利润为960万元.
由2000-960=1040(万元)知:还需另筹资金1040万元可解决温饱问题.
(2)2005年为第9年,该年可从两个企业获得利润

 >20×81×5=8100
>20×81×5=8100所以该乡到2005年底可以达到小康水平.
点评:本题考查的重点是解决实际问题,解题的关键是构建函数模型,利用基本不等式解决最值问题,属于中档题.

练习册系列答案
相关题目
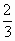 ,根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
,根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.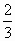 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.