题目内容
对于函数f(x)=(x2-2x)ex有以下4个命题:
①f(x)有最大值,但无最小值;
②f(x)有最小值,但无最大值;
③f(x))既有极大值,也有极小值;
④f(x)既无最大值,也无最小值.
则真命题的序号是________.(把所有真命题的序号都填上)
③
分析:由f(x)=(x2-2x)ex的定义域是R,f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,令f′(x)=0,得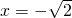 ,
,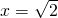 ,列表讨论,得f(x)既有极大值,也有极小值;f(x)既无最大值,也无最小值.
,列表讨论,得f(x)既有极大值,也有极小值;f(x)既无最大值,也无最小值.
解答:∵f(x)=(x2-2x)ex的定义域是R,
f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,
∴令f′(x)=0,得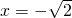 ,
,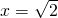 ,
,
列表:
x (-∞,- )-
)- (-
(-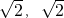 )
)  (
(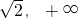 ) f(x)+ 0- 0+ f′(x)↑ 极大值↓ 极小值↑所以f(x)既有极大值,也有极小值.
) f(x)+ 0- 0+ f′(x)↑ 极大值↓ 极小值↑所以f(x)既有极大值,也有极小值.
故答案为:③.
点评:本题考查利用导数求闭区间上函数最值的应用,是基础题.解题时要认真审题,仔细解答,注意导数性质的灵活运用.
分析:由f(x)=(x2-2x)ex的定义域是R,f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,令f′(x)=0,得
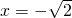 ,
,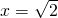 ,列表讨论,得f(x)既有极大值,也有极小值;f(x)既无最大值,也无最小值.
,列表讨论,得f(x)既有极大值,也有极小值;f(x)既无最大值,也无最小值.解答:∵f(x)=(x2-2x)ex的定义域是R,
f′(x)=(2x-2)ex+(x2-2x)ex=(x2-2)ex,
∴令f′(x)=0,得
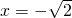 ,
,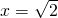 ,
,列表:
x (-∞,-
 )-
)- (-
(-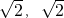 )
)  (
(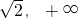 ) f(x)+ 0- 0+ f′(x)↑ 极大值↓ 极小值↑所以f(x)既有极大值,也有极小值.
) f(x)+ 0- 0+ f′(x)↑ 极大值↓ 极小值↑所以f(x)既有极大值,也有极小值.故答案为:③.
点评:本题考查利用导数求闭区间上函数最值的应用,是基础题.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目