题目内容
已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(Ⅱ)确定x,y,z的值,使成本最低.
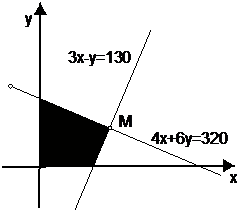 解:(I)∵某食物营养所想用x千克甲种食物,y千克乙种食物,z千克丙种食物配成100千克混合物,
解:(I)∵某食物营养所想用x千克甲种食物,y千克乙种食物,z千克丙种食物配成100千克混合物,∴Z=100-x-y,
∴C=11x+9y+4z=11x+9y+4(100-x-y)=7x+5y+400元;
(II)由题意可得:
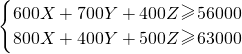 ,
,又∵Z=100-X-Y,
所以
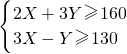 ,
,所以C=400+7X+5Y
=400+2(2X+3)+3X-Y≥850,
当且仅
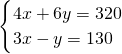 ,即
,即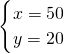 时等号成立.
时等号成立.所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
分析:(I)根据题意得出Z=100-X-Y,再利用甲.乙.丙三种食物的成本求出即可;
(II)根据题意得出600X+700Y+400Z≥5600,800X+400Y+500Z≥6300,再利用Z=100-X-Y,得出当且仅当2X+3=160,3X-Y=130时成立,求出X,Y,Z即可.
点评:此题主要考查了简单线性规划的应用.根据已知得出不等式关系式,求出关于X,Y的不等式组成立的条件是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
已知甲、乙、丙三种食物的维生素A、B含量及成本如下表:
现分别用甲、乙、丙三种食物配成10kg混合食物,并使混合食物内至少含有560单位维生素A和630单位维生素B.
(1)若混合食物中恰含580单位维生素A和660单位维生素B,求混合食物的成本为多少元?
(2)分别用甲、乙、丙三种食物各多少千克,才能使混合食物的成本最低?最低成本为多少元?
| 甲 | 乙 | 丙 | |
| 维生素A(单位/kg) | 60 | 70 | 40 |
| 维生素B(单位/kg) | 80 | 40 | 50 |
| 成本(元/kg) | 11 | 9 | 4 |
(1)若混合食物中恰含580单位维生素A和660单位维生素B,求混合食物的成本为多少元?
(2)分别用甲、乙、丙三种食物各多少千克,才能使混合食物的成本最低?最低成本为多少元?
已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用
甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物
内至少含有56000单位维生素A和63000单位维生素B.
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(1)用x,y表示混合食物成本c元;
(2)确定x,y,z的值,使成本最低.
(本小题满分12分)已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(Ⅱ)确定x,y,z的值,使成本最低.
.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
|
|
甲 |
乙 |
丙 |
|
维生素A(单位/千克) |
600 |
700 |
400 |
|
维生素B(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
(Ⅰ)用x,y表示混合食物成本c元;
(Ⅱ)确定x,y,z的值,使成本最低.