题目内容
给出如下命题:①直线
 是函数
是函数 的一条对称轴;
的一条对称轴;②函数f(x)关于点(3,0)对称,满足f(6+x)=f(6-x),且当x∈[0,3]时,函数为增函数,则f(x)在[6,9]上为减函数;
③命题“对任意a∈R,方程x2+ax-1=0有实数解”的否定形式为“存在a∈R,方程x2+ax-1=0无实数解”;
④lg25+lg2•lg50=1.
以上命题中正确的是 .
【答案】分析:首先分析命题①因为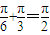 ,所以函数
,所以函数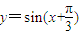 的一条对称轴方程是:
的一条对称轴方程是: .故命题①正确.
.故命题①正确.
分析命题②可以根据已知条件得函数f(x)满足f(6+x)=f(6-x),所以有函数f(x)在[6,9]的函数图象与函数在[3,6]上的图象关于x=6对称,又x∈[0,3]时,函数为增函数,所以函数在[3,6]区间上也为增函数,根据图象关系即可得出命题②正确.
分析③命题;根据命题否定的定义,对命题③的条件和结果都进行否定即可.
分析命题④,把左边式子根据对数的性质化简即可得到答案.
解答:解:对于①直线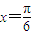 是函数
是函数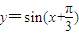 的一条对称轴;因为
的一条对称轴;因为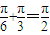 ,所以函数
,所以函数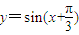 的一条对称轴方程是:
的一条对称轴方程是: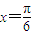 .故命题①正确.
.故命题①正确.
对于②命题“因为函数f(x)满足f(6+x)=f(6-x),所以有f(x)=f(12-x),
∵当x∈[0,3]时,函数f(x)为增函数,又函数f(x)关于点(3,0)对称,∴函数f(x)在[3,6]上也为增函数,从而函数在[0,6]上为增函数,
∵f(x)=f(12-x),函数f(x)的对称轴为x=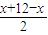 =6,
=6,
由函数的对称性可知,函数f(x)在区间[6,12]上为减函数,
∴f(x)在[6,9]上为减函数;故②正确;
对于③命题“对任意a∈R,方程x2+ax-1=0有实数解”的否定形式为“存在a∈R,方程x2+ax-1=0无实数解”;
此是一个全称命题的否定
∴命题的否定形式为:存在a∈R,方程x2+ax-1=0无实数解,故③正确;
对于④lg25+lg2•lg50=1.因为lg25+lg2•lg50=lg25+lg2(lg5+1)=lg5(lg5+lg2)+lg2=lg5+lg2=1.故命题④正确.
以上命题中正确的有①②③④.
故答案为①②③④.
点评:此题主要考查函数关于点对称,三角函数性质问题,命题的否定形式,和对数函数性质.这类题型在高考中属于易错题,考查的知识点较多,同学们做题的时候需要注意.
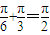 ,所以函数
,所以函数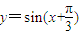 的一条对称轴方程是:
的一条对称轴方程是: .故命题①正确.
.故命题①正确.分析命题②可以根据已知条件得函数f(x)满足f(6+x)=f(6-x),所以有函数f(x)在[6,9]的函数图象与函数在[3,6]上的图象关于x=6对称,又x∈[0,3]时,函数为增函数,所以函数在[3,6]区间上也为增函数,根据图象关系即可得出命题②正确.
分析③命题;根据命题否定的定义,对命题③的条件和结果都进行否定即可.
分析命题④,把左边式子根据对数的性质化简即可得到答案.
解答:解:对于①直线
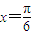 是函数
是函数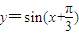 的一条对称轴;因为
的一条对称轴;因为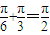 ,所以函数
,所以函数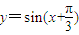 的一条对称轴方程是:
的一条对称轴方程是: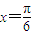 .故命题①正确.
.故命题①正确.对于②命题“因为函数f(x)满足f(6+x)=f(6-x),所以有f(x)=f(12-x),
∵当x∈[0,3]时,函数f(x)为增函数,又函数f(x)关于点(3,0)对称,∴函数f(x)在[3,6]上也为增函数,从而函数在[0,6]上为增函数,
∵f(x)=f(12-x),函数f(x)的对称轴为x=
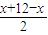 =6,
=6,由函数的对称性可知,函数f(x)在区间[6,12]上为减函数,
∴f(x)在[6,9]上为减函数;故②正确;
对于③命题“对任意a∈R,方程x2+ax-1=0有实数解”的否定形式为“存在a∈R,方程x2+ax-1=0无实数解”;
此是一个全称命题的否定
∴命题的否定形式为:存在a∈R,方程x2+ax-1=0无实数解,故③正确;
对于④lg25+lg2•lg50=1.因为lg25+lg2•lg50=lg25+lg2(lg5+1)=lg5(lg5+lg2)+lg2=lg5+lg2=1.故命题④正确.
以上命题中正确的有①②③④.
故答案为①②③④.
点评:此题主要考查函数关于点对称,三角函数性质问题,命题的否定形式,和对数函数性质.这类题型在高考中属于易错题,考查的知识点较多,同学们做题的时候需要注意.

练习册系列答案
相关题目
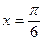 是函数
是函数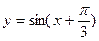 的一条对称轴;
的一条对称轴;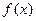 关于点(3,0)对称,满足
关于点(3,0)对称,满足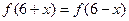 ,且当
,且当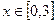 时,函数为增函数,则
时,函数为增函数,则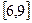 上为减函数;
上为减函数;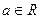 ,方程
,方程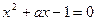 有实数解”的否定形式为“存在
有实数解”的否定形式为“存在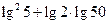
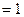
 是 .
是 .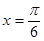 是函数
是函数 的一条对称轴;
的一条对称轴;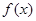 关于点(3,0)对称,满足
关于点(3,0)对称,满足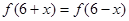 ,且当
,且当 时,函数为增函数,则
时,函数为增函数,则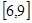 上为减函数;
上为减函数;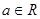 ,方程
,方程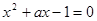 有实数解”的否定形式为“存在
有实数解”的否定形式为“存在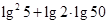
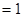
 是
是
 是函数
是函数 的一条对称轴;
的一条对称轴;