题目内容
(理)某3上男同学和3个女同学站成一排照相,要求任何相邻的两位同学性别
不同,且男生甲和女生乙相邻,但甲和乙都不站两端,则不同的站法种数是 ( )
不同,且男生甲和女生乙相邻,但甲和乙都不站两端,则不同的站法种数是 ( )
| A.8 | B.16 | C.20 | D.24 |
D
考点:
分析:根据题意的要求任何相邻的两位同学性别不同,分析可得男生与女生必须相间,即要先把男生与女生分别分析,将其排好之后,再进行分插;按甲在男生中所站的位置不同,分两种情况讨论,①、甲在男生的中间,②、甲在男生的左边或右边;分别求出其中所有的站法数目,由加法原理计算可得答案.
解答:解:根据题意,要求任何相邻的两位同学性别不同,男生与女生必须相间,
按甲所站的位置不同,分两种情况讨论,
①、甲在男生的中间,其余的男生有2种站法,即男生共2种站法;
此时女生乙在女生中的站法有3种,若乙在左边或右边时,其余的女生2种站法,与男生有一种相间的方法,若乙在中间,其余的女生2种站法,与男生有二种相间的方法,则此时共2×(2×2×1+2×2)=16种;
②、甲在男生的左边或右边时,其余的男生有2种站法,即男生共2种站法;此生女生乙必须在女生的中间,其余的女生2种站法,与男生有二种相间的方法,此时,共2×2×2=8种站法;综合可得:共16+8=24种站法;
故选D.
点评:本题考查排列组合的综合运用,解题时,注意常见问题的处理方法,如相邻问题用捆绑法,不相邻问题用插空法等.
分析:根据题意的要求任何相邻的两位同学性别不同,分析可得男生与女生必须相间,即要先把男生与女生分别分析,将其排好之后,再进行分插;按甲在男生中所站的位置不同,分两种情况讨论,①、甲在男生的中间,②、甲在男生的左边或右边;分别求出其中所有的站法数目,由加法原理计算可得答案.
解答:解:根据题意,要求任何相邻的两位同学性别不同,男生与女生必须相间,
按甲所站的位置不同,分两种情况讨论,
①、甲在男生的中间,其余的男生有2种站法,即男生共2种站法;
此时女生乙在女生中的站法有3种,若乙在左边或右边时,其余的女生2种站法,与男生有一种相间的方法,若乙在中间,其余的女生2种站法,与男生有二种相间的方法,则此时共2×(2×2×1+2×2)=16种;
②、甲在男生的左边或右边时,其余的男生有2种站法,即男生共2种站法;此生女生乙必须在女生的中间,其余的女生2种站法,与男生有二种相间的方法,此时,共2×2×2=8种站法;综合可得:共16+8=24种站法;
故选D.
点评:本题考查排列组合的综合运用,解题时,注意常见问题的处理方法,如相邻问题用捆绑法,不相邻问题用插空法等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
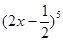 的展开式中
的展开式中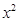 的系数是 ( )
的系数是 ( )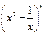 展开式中的二项式系数的和比
展开式中的二项式系数的和比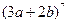 展开式的二项式系数的和大
展开式的二项式系数的和大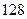 ,求
,求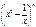 展开式中的系数最大的项和系数最小的项.
展开式中的系数最大的项和系数最小的项.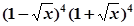 的展开式中
的展开式中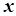 的系数是( )
的系数是( )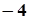
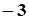
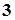
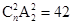 ,则
,则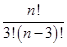 的值为 ( )
的值为 ( )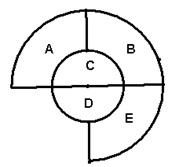
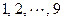 的
的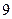 个小正方形(如下图),
个小正方形(如下图),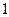 、
、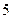 、
、