题目内容
数列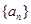 的通项
的通项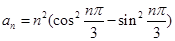 ,其前
,其前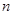 项和为
项和为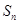 ,则
,则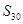 为 .
为 .
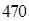
解析试题分析: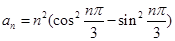 即
即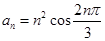 ,随n的取值1,2,3,……,
,随n的取值1,2,3,……,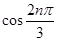 依次为-
依次为-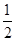 ,-
,-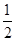 ,1,-
,1,-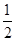 ,-
,-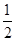 ,1,……,重复出现,
,1,……,重复出现,
所以S30=12•cos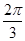 +22cos
+22cos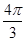 +32cos2π+……+302cos20π
+32cos2π+……+302cos20π
=-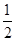 ×1-
×1-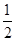 ×22+32-
×22+32-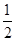 ×42-
×42-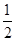 ×52+62+…-
×52+62+…-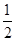 ×282-
×282-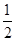 ×292+302
×292+302
=-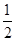 [1+22-2×32)+(42+52-62×2)+…+(282+292-302×2)]
[1+22-2×32)+(42+52-62×2)+…+(282+292-302×2)]
=-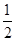 [(12-33)+(42-62)+…+(282-302)+(22-32)+(52-62)+…+(292-302)]
[(12-33)+(42-62)+…+(282-302)+(22-32)+(52-62)+…+(292-302)]
=-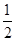 [-2(4+10+16…+58)-(5+11+17+…+59)]
[-2(4+10+16…+58)-(5+11+17+…+59)]
=-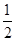 [-2×
[-2×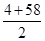 ×10-
×10-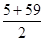 ×10] =470。
×10] =470。
考点:本题主要考查二倍角的余弦公式,等差数列的求和。
点评:中档题,本题解的思路比较明确,关键是发现余弦值呈现的周期性。求和过程中,灵活运用平方差公式,是进一步解题的又一关键步骤。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,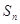 是它的前
是它的前 项之和,且
项之和,且 则
则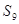 一定小于
一定小于
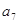 是各项中最大的一项 ④
是各项中最大的一项 ④ 一定是
一定是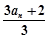 且a1=0,则a7= .
且a1=0,则a7= . 满足
满足 ,
, ,则
,则 ________.
________.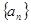 的前n项和为
的前n项和为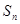 ,若
,若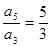 ,则
,则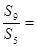 。
。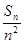 ,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________.
,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________. }是等差数列,
}是等差数列,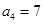 ,则
,则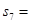 _________
_________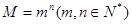 的正整数表示成各项都是整数,公差为2的等差数列前
的正整数表示成各项都是整数,公差为2的等差数列前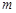 项的和,称作“对
项的和,称作“对 的
的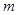 项分划”,例如:
项分划”,例如: ,称作“对9的3项分划”;
,称作“对9的3项分划”;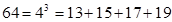 称作“对64的4项分划”,据此对324的18项分划中最大的数是
称作“对64的4项分划”,据此对324的18项分划中最大的数是  的前
的前 项和为
项和为 ,则
,则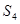 ,
,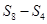 ,
,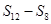 ,
,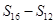 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列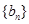 的前
的前 ,则
,则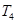 , ,______,
, ,______,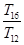 成等比数列.
成等比数列.