题目内容
(本小题满分10分)在△ABC中,a、b是方程x2-2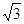 x+2=0的两根,
x+2=0的两根,
且2cos(A+B)=-1.(1)求角C的度数; (2)求c; (3)求△ABC的面积.
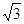 x+2=0的两根,
x+2=0的两根,且2cos(A+B)=-1.(1)求角C的度数; (2)求c; (3)求△ABC的面积.
解:(1)∵2cos(A+B)=1,∴cosC=-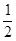 .∴角C的度数为120°.
.∴角C的度数为120°.
(2)∵a、b是方程x2-2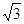 x+2=0的两根,∴a+b=2
x+2=0的两根,∴a+b=2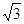 ,ab=2,
,ab=2,
c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10.∴c=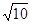 .
.
(3)S=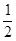 absinC=
absinC=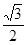 .
.
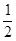 .∴角C的度数为120°.
.∴角C的度数为120°.(2)∵a、b是方程x2-2
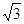 x+2=0的两根,∴a+b=2
x+2=0的两根,∴a+b=2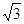 ,ab=2,
,ab=2,c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10.∴c=
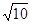 .
.(3)S=
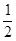 absinC=
absinC=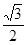 .
.略

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 中,角
中,角 所对应的边分别为
所对应的边分别为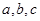 ,
,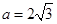 ,
,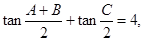
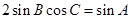 ,求
,求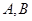 及
及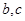 .
.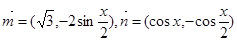 (
(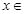 R),函数
R),函数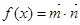 .
.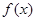 的值域;
的值域;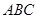 的内角
的内角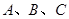 的对边长分别为
的对边长分别为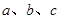 ,若
,若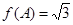 ,且
,且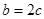 ,求角
,求角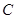 的值.
的值.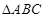 的面积
的面积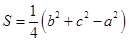 其中
其中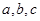 分别为角
分别为角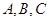 所对的边.
所对的边.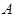 的大小;(2)若
的大小;(2)若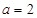 ,求
,求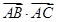 的最大值.
的最大值.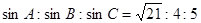 ,则角A =
,则角A =  ABC中.
ABC中.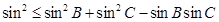 .则A的取值范围是( )
.则A的取值范围是( )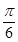 ] (B)[
] (B)[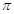 ) (c)(0,
) (c)(0,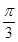 ] (D)[
] (D)[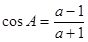 ,则实数a的取值范围是
,则实数a的取值范围是 ,则
,则 与
与 的大小关系为 ( )
的大小关系为 ( ) 
