题目内容
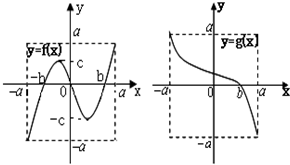
定义域和值域均为[-a,a]的函数y=f(x)和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个命题:
①方程f[g(x)]=0有且仅有三个解;
②方程g[f(x)]=0有且仅有三个解;
③方程f[f(x)]=0有且仅有九个解;
④方程g[g(x)]=0有且仅有一个解.
其中正确命题的个数是( )
①方程f[g(x)]=0有且仅有三个解;
②方程g[f(x)]=0有且仅有三个解;
③方程f[f(x)]=0有且仅有九个解;
④方程g[g(x)]=0有且仅有一个解.
其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |

①设t=g(x),则由f[g(x)]=0,即f(t)=0,当t=0时,则t=g(x)有三个不同值,由于y=g(x)是减函数,所有三个解,所以①正确.
②设t=f(x),若g[f(x)]=0,即g(t)=0,则t=b,所以f(x)=b,因为c>b>0,所以对应f(x)=b的解有3个,所以②正确.
③设t=f(x),若f[f(x)]=0,即f(t)=0,t=-b或t=0或t=b,则f(x)=-b,或f(x)=0,或f(x)=b,因为a>c>b>0,所以每个方程对应着三个解,所以共9个解,所以③正确.
④设t=g(x),若g[g(x)]=0,即g(t)=0,所以t=b,则g(x)=b,因为y=g(x)是减函数,所以方程g(x)=b只有1解,所以④正确.
故选D.
②设t=f(x),若g[f(x)]=0,即g(t)=0,则t=b,所以f(x)=b,因为c>b>0,所以对应f(x)=b的解有3个,所以②正确.
③设t=f(x),若f[f(x)]=0,即f(t)=0,t=-b或t=0或t=b,则f(x)=-b,或f(x)=0,或f(x)=b,因为a>c>b>0,所以每个方程对应着三个解,所以共9个解,所以③正确.
④设t=g(x),若g[g(x)]=0,即g(t)=0,所以t=b,则g(x)=b,因为y=g(x)是减函数,所以方程g(x)=b只有1解,所以④正确.
故选D.

练习册系列答案
相关题目
若函数f(x)=log2
的定义域和值域均为[1,+∞),则实数a的取值集合为( )
| x2+ax+1 |
| x |
| A、{0} |
| B、{a|0≤a≤1} |
| C、{a|a≥0} |
| D、{a|a≥2} |
