题目内容
定义运算符号:“π”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作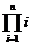 ,(n∈N*),记Tn=
,(n∈N*),记Tn=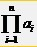 ,其中ai为数列{an}(n∈N*)中的第i项.
,其中ai为数列{an}(n∈N*)中的第i项.
①若an=3n-2,则T4=
②若Tn=2n2(n∈N*),则an=
.
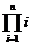 ,(n∈N*),记Tn=
,(n∈N*),记Tn=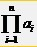 ,其中ai为数列{an}(n∈N*)中的第i项.
,其中ai为数列{an}(n∈N*)中的第i项.①若an=3n-2,则T4=
280
280
;②若Tn=2n2(n∈N*),则an=
|
|
分析:①根据an=3n-2,分别令n=1,2,3,4求得a1=1,a2=4,a3=7,a4=10,求得T4的值;
②由Tn=2n2,可令n=1,n≥2时讨论求解,n≥2时,an=
从而可求出所求.
②由Tn=2n2,可令n=1,n≥2时讨论求解,n≥2时,an=
| Tn |
| Tn-1 |
解答:解:①∵an=3n-2,∴a1=1,a2=4,a3=7,a4=10,
T4=1×4×7×10=280;
②∵Tn=2n2
∴当n=1时,a1=2,
当n≥2时,an=
=
=
,
∴an=
.
故答案为:280;an=
.
T4=1×4×7×10=280;
②∵Tn=2n2
∴当n=1时,a1=2,
当n≥2时,an=
| Tn |
| Tn-1 |
| 2n2 |
| 2(n-1)2 |
| n2 |
| (n-1)2 |
∴an=
|
故答案为:280;an=
|
点评:本题主要考查数列的性质和应用,以及知识方法的迁移能力,(与已知数列的前n项和,求数列的通项公式的方法是相同的),体现分类讨论的思想,属中档题.

练习册系列答案
相关题目

 =1×2×3×…×n.记Tn=
=1×2×3×…×n.记Tn= ,其中ai为数列{an}中的第i项.
,其中ai为数列{an}中的第i项. ”:表示若干个数相乘,例如:
”:表示若干个数相乘,例如: .记
.记 ,
,  为数列
为数列 中的第
中的第 项.
项. ,则
,则 ;
; ,则
,则 .
. ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作 ,
, ,其中
,其中 为数列
为数列 中的第
中的第 项.
项. ,则
,则 = ; ②若
= ; ②若