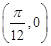题目内容
定义行列式运算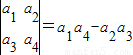 ,将函数
,将函数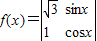 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )A.
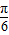
B.
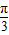
C.
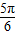
D.
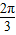
【答案】分析:先根据题意确定函数f(x)的解析式,然后根据左加右减的原则得到平移后的解析式,再根据偶函数的性质可确定n的值.
解答:解:由题意可知f(x)=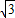 cosx-sinx=2cos(x+
cosx-sinx=2cos(x+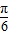 )
)
将函数f(x)的图象向左平移n(n>0)个单位后得到y=2cos(x+n+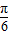 )为偶函数
)为偶函数
∴2cos(-x+n+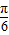 )=2cos(x+n+
)=2cos(x+n+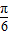 )
)
∴cosxcos(n+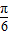 )+sinxsin(n+
)+sinxsin(n+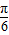 )=cosxcos(n+
)=cosxcos(n+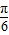 )-sinxsin(n+
)-sinxsin(n+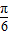 )
)
∴sinxsin(n+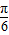 )=-sinxsin(n+
)=-sinxsin(n+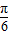 )
)
∴sinxsin(n+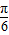 )=0∴sin(n+
)=0∴sin(n+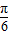 )=0∴n+
)=0∴n+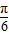 =kπ
=kπ
∴n=-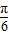 +kπ
+kπ
n大于0的最小值等于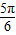
故选C.
点评:本题主要考查两角和与差的余弦公式、三角函数的奇偶性和平移变换.平移时根据左加右减上加下减的原则进行平移.
解答:解:由题意可知f(x)=
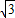 cosx-sinx=2cos(x+
cosx-sinx=2cos(x+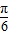 )
)将函数f(x)的图象向左平移n(n>0)个单位后得到y=2cos(x+n+
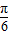 )为偶函数
)为偶函数∴2cos(-x+n+
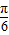 )=2cos(x+n+
)=2cos(x+n+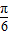 )
)∴cosxcos(n+
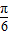 )+sinxsin(n+
)+sinxsin(n+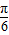 )=cosxcos(n+
)=cosxcos(n+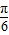 )-sinxsin(n+
)-sinxsin(n+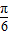 )
)∴sinxsin(n+
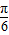 )=-sinxsin(n+
)=-sinxsin(n+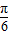 )
)∴sinxsin(n+
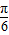 )=0∴sin(n+
)=0∴sin(n+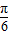 )=0∴n+
)=0∴n+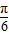 =kπ
=kπ∴n=-
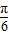 +kπ
+kπn大于0的最小值等于
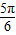
故选C.
点评:本题主要考查两角和与差的余弦公式、三角函数的奇偶性和平移变换.平移时根据左加右减上加下减的原则进行平移.

练习册系列答案
相关题目
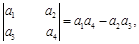 将函数
将函数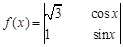 的图象向左平移
的图象向左平移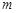 个单位
个单位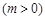 ,若所得图象对应的函数为偶函数,则
,若所得图象对应的函数为偶函数,则 B.
B.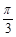 C.
C.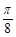 D.
D.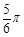
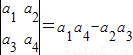 ,将函数
,将函数 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )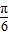
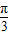
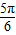
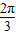
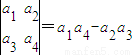 ,将函数
,将函数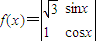 的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )
的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为( )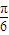
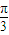
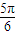
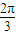
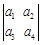 =
=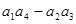 .将函数
.将函数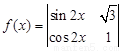 的图象向左平移
的图象向左平移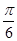 个单位,以下是所得函数图象的一个对称中心是
个单位,以下是所得函数图象的一个对称中心是 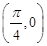 B.
B.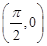 C.
C.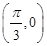 D.
D.