题目内容
16.某校为了解学生一次考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下:
90 71 64 66 72 39 49 46 55 56 85 52 6l
80 66 67 78 70 51 65 42 73 77 58 67

(1)请根据数据在答题卡的茎叶图中完成物理成绩统计如图1;
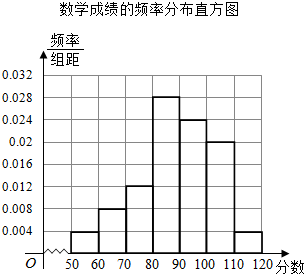
(2)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图如图2;
数学成绩的频数分布表如下表:
| 数学成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) | [110,120] |
| 频数 |
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(x1-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)=5524,$\frac{4698}{5524}$≈0.85
求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{1}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)根据所给数据,可得物理成绩的茎叶图;
(2)根据所给数据,可得数学成绩的频数分布表及数学成绩的频率分布直方图;
(3)求出a,b,可得y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩
解答 解:(1)物理成绩的茎叶图如图所示;
(2)数学成绩的频数分布表;
| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 | 1 | 2 | 3 | 7 | 6 | 5 | 1 |
(3)由已知得b=0.85,a=64-0.85×86=-9.1,
∴y=0.85x-9.1,
∴x=100时,y=75.9≈76,
预测当某考生的数学成绩为100分时,该考生的物理成绩为76分.
点评 本题考查茎叶图、数学成绩的频数分布表及数学成绩的频率分布直方图,考查线性回归方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
11.已知f(x)=ax5+bx3+sinx-8且f(-2)=10,那么f(2)=( )
| A. | -26 | B. | 26 | C. | -10 | D. | 10 |
8.下图中的图形经过折叠不能围成棱柱的是( )
| A. |  | B. |  | C. |  | D. |  |
5.若p的否命题是命题q的逆否命题,则命题p是命题q的( )
| A. | 逆命题 | B. | 否命题 | C. | 逆否命题 | D. | p与q是同一命题 |
6.已知集合P={x∈Z||x-1|<2},Q={x∈Z|-1≤x≤2},则P∩Q=( )
| A. | {0,1,2} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {1,2} |
