题目内容
设a>0,b>0,给出下列命题:
①若2a+2a=2b+3b,则a>b; ②若2a+2a=2b+3b,则a<b;
③若2a-2a=2b-3b,则a>b; ④若2a-2a=2b-3b,则a<b;
其中真命题是
①若2a+2a=2b+3b,则a>b; ②若2a+2a=2b+3b,则a<b;
③若2a-2a=2b-3b,则a>b; ④若2a-2a=2b-3b,则a<b;
其中真命题是
①
①
.(填序号)分析:利用导数得出函数的单调性和图象,进而即可得出结论.
解答:解:对于①②考查函数f(x)=2x+2x,g(x)=2x+3x的单调性与图象:
可知函数f(x)、g(x)在R上都单调递增,
若2a+2a=2b+3b,则a>b,因此①正确;
对于③④分别考查函数u(x)=2x-2x,v(x)=2x-3x单调性与图象:
u′(x)=ln2(2x-
),当0<x<log2
时,u′(x)<0,函数u(x)单调递减;当x>log2
时,u′(x)>0,函数u(x)单调递增.
故在x=log2
取得最小值-
.
v′(x)=ln2(2x-
),当0<x<log2
时,v′(x)<0,函数v(x)单调递减;当x>log2
时,v′(x)>0,函数v(x)单调递增.
故在x=log2
取得最小值-
.
据以上可画出图象.
据图象可知:
当2a-2a=2b-3b,a>0,b>0时,
可能a>b或a<b.
因此③④不正确.
综上可知:只有①正确.
故答案为①.

可知函数f(x)、g(x)在R上都单调递增,
若2a+2a=2b+3b,则a>b,因此①正确;
对于③④分别考查函数u(x)=2x-2x,v(x)=2x-3x单调性与图象:
u′(x)=ln2(2x-
| 2 |
| ln2 |
| 2 |
| ln2 |
| 2 |
| ln2 |
故在x=log2
| 2 |
| ln2 |
| 2 |
| ln2 |
v′(x)=ln2(2x-
| 3 |
| ln2 |
| 3 |
| ln2 |
| 3 |
| ln2 |
故在x=log2
| 3 |
| ln2 |
| 6 |
| ln2 |

据以上可画出图象.
据图象可知:
当2a-2a=2b-3b,a>0,b>0时,
可能a>b或a<b.
因此③④不正确.
综上可知:只有①正确.
故答案为①.
点评:熟练利用导数研究函数的单调性和图象是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 ;C.
;C. ;
;

 .
.
 ;B.
;B. ;C.
;C.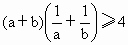 ;
; ;E.
;E. .
.