题目内容
函数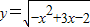
的递增区间为（ ）A．
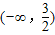
B．
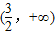
C．
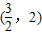
D．
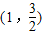
【答案】分析：先求出函数的定义域，然后令t=-x2+3x-2，将函数转化为y=
，再根据复合函数的同增异减性可求出其递增区间．
解答：解：∵-x2+3x-2≥0∴1≤x≤2
令t=-x2+3x-2，则y=
单调递增
∵t=-x2+3x-2的单调增区间是（-∞，
）
根据复合函数 的同增异减性可确定原函数的单调增区间为：（1，
）
故选D．
点评：本题主要考查复合函数的单调性、函数的定义域问题．考查对基础知识的理解和运用．
，再根据复合函数的同增异减性可求出其递增区间．解答：解：∵-x2+3x-2≥0∴1≤x≤2
令t=-x2+3x-2，则y=
单调递增∵t=-x2+3x-2的单调增区间是（-∞，
）根据复合函数 的同增异减性可确定原函数的单调增区间为：（1，
）故选D．
点评：本题主要考查复合函数的单调性、函数的定义域问题．考查对基础知识的理解和运用．
练习册系列答案
相关题目
在（0，+∞）上是增函数，（
，0）上也是增函数，所以
是增函数；
的递增区间为
； 
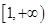则
；
的图象与函数y=log3x的图象关于直线y=x对称；
导函数的图象如图所示,则下列说法正确的是: 
处取得极大值 
处取得极小值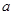
是实数．若函数
是定义在
上的奇函数，但不是偶函数，则函数
的递增区间为
．
； （2）已知
则
；
的图象与函数
的图象关于原点对称；
是偶函数；
的递增区间为
.