题目内容
底面边长为 ,各侧面均为直角三角形的正三棱锥的四个顶点都在同一球面上,则此球的表面积为( )
,各侧面均为直角三角形的正三棱锥的四个顶点都在同一球面上,则此球的表面积为( )A.4π
B.

C.2π
D.3π
【答案】分析:底面边长为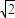 ,各侧面均为直角三角形的正三棱锥可以看作是正方体的一个角,故此正三棱锥的外接求即此正方体的外接球,由此求出正方体的体对角线即可得到球的直径,表面积易求
,各侧面均为直角三角形的正三棱锥可以看作是正方体的一个角,故此正三棱锥的外接求即此正方体的外接球,由此求出正方体的体对角线即可得到球的直径,表面积易求
解答:解:由题意知此正三棱锥的外接球即是相应的正方体的外接球,此正方体的面对角线为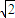 ,边长为1.
,边长为1.
正方体的体对角线是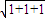 =
=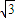 .
.
故外接球的直径是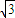 ,半径是
,半径是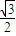 .
.
故其表面积是4×π× =3π.
=3π.
故选D.
点评:本题考查球内接多面体,解题的关键是找到球的直径与其内接多面体的量之间的关系,由此关系求出球的半径进而得到其表面积
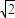 ,各侧面均为直角三角形的正三棱锥可以看作是正方体的一个角,故此正三棱锥的外接求即此正方体的外接球,由此求出正方体的体对角线即可得到球的直径,表面积易求
,各侧面均为直角三角形的正三棱锥可以看作是正方体的一个角,故此正三棱锥的外接求即此正方体的外接球,由此求出正方体的体对角线即可得到球的直径,表面积易求解答:解:由题意知此正三棱锥的外接球即是相应的正方体的外接球,此正方体的面对角线为
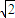 ,边长为1.
,边长为1.正方体的体对角线是
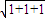 =
=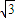 .
.故外接球的直径是
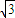 ,半径是
,半径是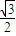 .
.故其表面积是4×π×
 =3π.
=3π.故选D.
点评:本题考查球内接多面体,解题的关键是找到球的直径与其内接多面体的量之间的关系,由此关系求出球的半径进而得到其表面积

练习册系列答案
相关题目