题目内容
若对于任意角θ,都有asinθ-bcosθ=1(ab≠0),则下列不等式中恒成立的是( )
A、
| ||||
| B、a2+b2≤1 | ||||
C、
| ||||
| D、a2+b2≥1 |
分析:对已知表达式平方化简,利用同角三角函数的基本关系式化简,得到a2+b2=1+(bsinθ+acosθ)2,推出结论.
解答:解:等式两边平方的a2sin2θ+b2cos2θ-2absinθcosθ=1,a2sin2θ+a2cos2θ+b2cos2θ+b2sin2θ-(2absinθcosθ+a2cos2θ+b2sin2θ)=1,
a2+b2-(bsinθ+acosθ)2=1,a2+b2=1+(bsinθ+acosθ)2所以a2+b2≥1
故选D
a2+b2-(bsinθ+acosθ)2=1,a2+b2=1+(bsinθ+acosθ)2所以a2+b2≥1
故选D
点评:本题是基础题,考查三角函数的最值,基本不等式的应用,考查计算能力,逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,都有
,都有 ,则下列不等式中恒成立的是
,则下列不等式中恒成立的是
 B.
B.  C.
C.  D.
D. 
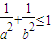
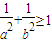
 ,则下列不等式中恒成立的是
,则下列不等式中恒成立的是 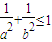 D.
D. .
.