题目内容
在等比数列中,各项均为正数,且a2a6=9,则log
(a3a4a5)= .
| 1 | 3 |
分析:由等比数列的性质结合已知条件求出a4及a3a5的值,代入log
(a3a4a5)后由对数式的运算性质得答案.
| 1 |
| 3 |
解答:解:∵数列{an}是各项均为正数的等比数列,且a2a6=9,
∴a42=a3a5=a2a6=9,∴a4=3.
则a3a4a5=27.
∴log
(a3a4a5)=log
27=-3.
故答案为:-3.
∴a42=a3a5=a2a6=9,∴a4=3.
则a3a4a5=27.
∴log
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:-3.
点评:本题考查了等比数列的通项公式,考查了对数的运算性质,是基础的计算题.

练习册系列答案
相关题目
 中,各项均为正数,且
中,各项均为正数,且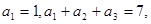 则数列
则数列 。
。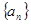 中,各项均为正数,且
中,各项均为正数,且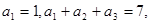 则数列
则数列