题目内容
如图,设A、B、C是球O面上的三点,我们把大圆的劣弧 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、C-OB-A、A-OC-B的大小分别为α、β、γ,给出下列命题:
①若
 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
;②若
 ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
;③圆弧
 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;④若a=b,则α=β.
其中你认为正确的所有命题的序号是 .

【答案】分析:由 ,知球面三角形ABC是
,知球面三角形ABC是 球体,故球面三角形ABC的面积=
球体,故球面三角形ABC的面积= =
= ;由
;由 ,知四面体OABC的面积=3×
,知四面体OABC的面积=3× =
= ,;圆弧
,;圆弧 在点A处的切线l1在OAB面上与OA垂直,圆弧
在点A处的切线l1在OAB面上与OA垂直,圆弧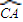 在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β.
在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β.
解答:解:∵ ,
,
∴球面三角形ABC是 球体,
球体,
∴球面三角形ABC的面积=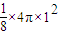 =
= .
.
故①正确;
∵ ,
,
∴四面体OABC的侧面积=3× =
=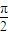 ,
,
故②正确;
∵圆弧 在点A处的切线l1在OAB面上与OA垂直,
在点A处的切线l1在OAB面上与OA垂直,
圆弧 在点A处的切线l2在OAC面上与OA垂直,
在点A处的切线l2在OAC面上与OA垂直,
∴l1与l2夹角等于α,不一定等于a,
故③不正确;
若a=b,由图形的对称性知,α=β.故④正确.
故答案为:①②④.
点评:本题考查球面三角形的概率和应用,是基础题.解题时要认真审题,熟练掌握球球面三角形的性质和应用.
 ,知球面三角形ABC是
,知球面三角形ABC是 球体,故球面三角形ABC的面积=
球体,故球面三角形ABC的面积= =
= ;由
;由 ,知四面体OABC的面积=3×
,知四面体OABC的面积=3× =
= ,;圆弧
,;圆弧 在点A处的切线l1在OAB面上与OA垂直,圆弧
在点A处的切线l1在OAB面上与OA垂直,圆弧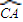 在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β.
在点A处的切线l2在OAC面上与OA垂直,故l1与l2夹角等于α;若a=b,则α=β.解答:解:∵
 ,
,∴球面三角形ABC是
 球体,
球体,∴球面三角形ABC的面积=
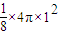 =
= .
.故①正确;
∵
 ,
,∴四面体OABC的侧面积=3×
 =
=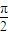 ,
,故②正确;
∵圆弧
 在点A处的切线l1在OAB面上与OA垂直,
在点A处的切线l1在OAB面上与OA垂直,圆弧
 在点A处的切线l2在OAC面上与OA垂直,
在点A处的切线l2在OAC面上与OA垂直,∴l1与l2夹角等于α,不一定等于a,
故③不正确;
若a=b,由图形的对称性知,α=β.故④正确.
故答案为:①②④.
点评:本题考查球面三角形的概率和应用,是基础题.解题时要认真审题,熟练掌握球球面三角形的性质和应用.

练习册系列答案
相关题目

 (2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧
(2010•成都一模)如图,设A、B、C是球O面上的三点,我们把大圆的劣弧
 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
; 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;
 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
; 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;