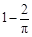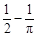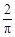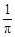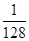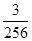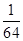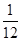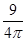题目内容
一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了 次球,则
次球,则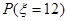 等于 ( )
等于 ( )
A.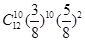 | B. | C.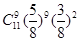 | D. |
B
解析试题分析:根据题意,由于一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,当取出12次球就停止了,说民最后一次取出的为红球,前11次有9次红球,则利用可放回的抽样可知,每次试验中抽到红球的概率为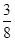 ,取到白球的概率为
,取到白球的概率为 ,则可知
,则可知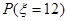 =
= ,故答案为B。
,故答案为B。
考点:二项分布的概率
点评:主要是考查了二项分布的概率的计算,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果随机变量§~N(—2,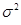 ),且P(—3≤§≤—1)=0.4,则P(§≥—1)=
),且P(—3≤§≤—1)=0.4,则P(§≥—1)=
| A.0.7 | B.0.6 | C.0.3 | D.0.2 |
已知随机变量X~B(n,0.8),D(X)=1.6,则n的值是
| A.8 | B.10 | C.12 | D.14 |
某事件 发生的概率为
发生的概率为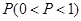 ,则事件
,则事件 在一次试验中发生的次数
在一次试验中发生的次数 的方差的最大值为( )
的方差的最大值为( )
A.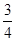 | B.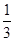 | C.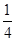 | D.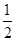 |
下图的程序框图中 是产生随机数的函数,它能随机产生区间
是产生随机数的函数,它能随机产生区间 内的任何一个数,如果输入N值为4000,输出的m值为1840,则利用随机模拟方法计算由
内的任何一个数,如果输入N值为4000,输出的m值为1840,则利用随机模拟方法计算由 与
与 及
及 轴所围成面积的近似值为( )
轴所围成面积的近似值为( )
| A.0.46 | B.2.16 | C.1.84 | D.0.54 |