题目内容
已知圆中一段弧长正好等于该圆的外切正三角形的边长，那么这段弧所对的圆心角的弧度数为 ( )
A． | B． | C． | D．2 |
D
解析试题分析：根据题意，由于设圆的半径为r，则可知，圆中一段弧长正好等于该圆的外切正三角形的边长，可知圆心到三角形不边长的距离为r，利用30得三角函数知可知，正三角形得边长得的长度为2r,那么利用弧长公式可知，弧度数等于弧长除以半径即为2，故选D.
考点：弧度数的问题
点评：解决的关键是根据弧长公式，利用圆的半径来得到弧度数，属于基础题。
练习册系列答案
相关题目
( )
A． | B． | C． | D． |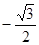
若角
的终边落在直线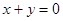
上，则
的值等于（ ）．
A． | B． | C．或 | D． |
如果函数
的最小正周期是
,且当
时取得最大值,那么（ ）
A． | B． | C． | D． |
函数y=
的最小正周期是（ ）
A． | B． | C．2 | D．4 |
已知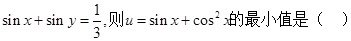
A． | B．-1 | C．1 | D． |
函数y=2cos2(x－
)－1是 ( )
| A．最小正周期为p的奇函数 | B．最小正周期为2p的奇函数 |
| C．最小正周期为p的偶函数 | D．最小正周期为2p的偶函数 |
下列命题正确的是（ ）
| A．第一象限的角一定不是负角 | B．小于90°的角一定是锐角 |
| C．钝角一定是第二象限的角 | D．终边相同的角一定相等 |
sin330°的值为( )
A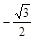． | B． | C． | D． |