题目内容
已知函数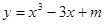 的图像与
的图像与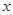 轴恰有两个公共点,则
轴恰有两个公共点,则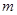 等于( )
等于( )
| A.-2或2 | B.-9或3 | C.-1或1 | D.-3或1 |
A
解析试题分析:求导函数,确定函数的单调性,确定函数的极值点,利用函数y=x3-3x+c的图象与x轴恰有两个公共点,可得极大值等于0或极小值等于0,由此可求m的值解:求导函数可得y′=3(x+1)(x-1),令y′>0,可得x>1或x<-1;令y′<0,可得-1<x<1;,∴函数在(-∞,-1),(1,+∞)上单调增,(-1,1)上单调减,∴函数在x=-1处取得极大值,在x=1处取得极小值,∵函数y=x3-3x+c的图象与x轴恰有两个公共点,∴极大值等于0或极小值等于0,∴1-3+c=0或-1+3+c=0,∴m=-2或2,故选A.
考点:导数的运用
点评:本题考查导数知识的运用,考查函数的单调性与极值,解题的关键是利用极大值等于0或极小值等于0.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是 ( )
的解集是 ( )
A. | B. |
C. | D. |
设函数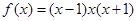 ,则满足
,则满足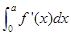 =0的实数a的有( )
=0的实数a的有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
若实数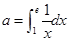 .则函数
.则函数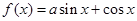 的图像的一条对称轴方程为
的图像的一条对称轴方程为
| A.x=0 | B.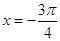 | C.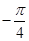 | D.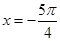 |
已知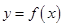 是定义在
是定义在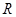 上的奇函数,且当x<0时不等式
上的奇函数,且当x<0时不等式 成立,若
成立,若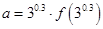 ,
, 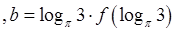
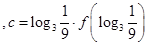 ,则
,则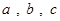 大小关系是
大小关系是
A.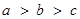 | B.c > b > a | C.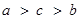 | D.c > a >b |
计算定积分 的值是( )
的值是( )
A.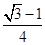 | B.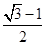 | C.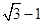 | D.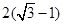 |
已知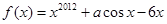 ,且
,且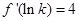 ,则
,则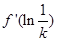 =( )
=( )
| A.-4 | B.4 | C.8 | D.-16 |
函数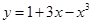 有( )
有( )
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-1,极大值3 | D.极小值-2,极大值2 |
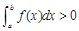 ,则f(x)>0; ⑵
,则f(x)>0; ⑵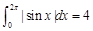 ;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则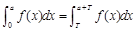 ;其中正确命题的个数为( )
;其中正确命题的个数为( )